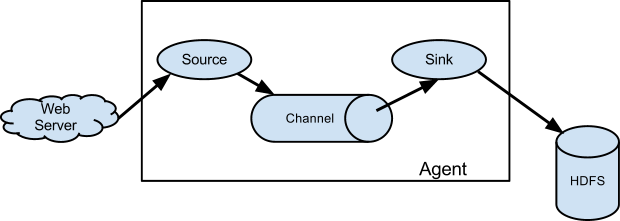
As mentioned in the earlier section, Flume agent configuration is read from a
file that resembles a Java property file format with hierarchical property
settings.
Fan out flow
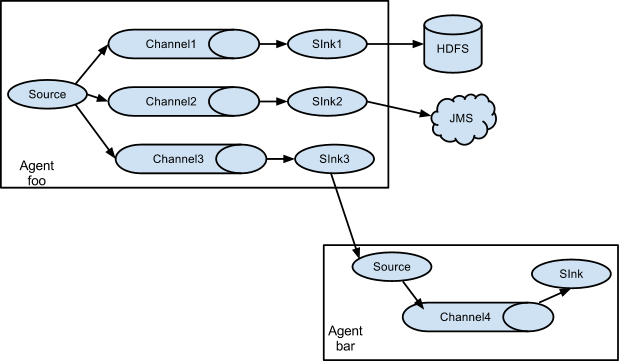
As discussed in previous section, Flume supports fanning out the flow from one
source to multiple channels. There are two modes of fan out, replicating and
multiplexing. In the replicating flow, the event is sent to all the configured
channels. In case of multiplexing, the event is sent to only a subset of
qualifying channels. To fan out the flow, one needs to specify a list of
channels for a source and the policy for the fanning it out. This is done by
adding a channel “selector” that can be replicating or multiplexing. Then
further specify the selection rules if it’s a multiplexer. If you don’t specify
a selector, then by default it’s replicating:
# List the sources, sinks and channels for the agent
<Agent>.sources = <Source1>
<Agent>.sinks = <Sink1> <Sink2>
<Agent>.channels = <Channel1> <Channel2>
# set list of channels for source (separated by space)
<Agent>.sources.<Source1>.channels = <Channel1> <Channel2>
# set channel for sinks
<Agent>.sinks.<Sink1>.channel = <Channel1>
<Agent>.sinks.<Sink2>.channel = <Channel2>
<Agent>.sources.<Source1>.selector.type = replicating
The multiplexing select has a further set of properties to bifurcate the flow.
This requires specifying a mapping of an event attribute to a set for channel.
The selector checks for each configured attribute in the event header. If it
matches the specified value, then that event is sent to all the channels mapped
to that value. If there’s no match, then the event is sent to set of channels
configured as default:
# Mapping for multiplexing selector
<Agent>.sources.<Source1>.selector.type = multiplexing
<Agent>.sources.<Source1>.selector.header = <someHeader>
<Agent>.sources.<Source1>.selector.mapping.<Value1> = <Channel1>
<Agent>.sources.<Source1>.selector.mapping.<Value2> = <Channel1> <Channel2>
<Agent>.sources.<Source1>.selector.mapping.<Value3> = <Channel2>
#...
<Agent>.sources.<Source1>.selector.default = <Channel2>
The mapping allows overlapping the channels for each value.
The following example has a single flow that multiplexed to two paths. The
agent named agent_foo has a single avro source and two channels linked to two sinks:
# list the sources, sinks and channels in the agent
agent_foo.sources = avro-AppSrv-source1
agent_foo.sinks = hdfs-Cluster1-sink1 avro-forward-sink2
agent_foo.channels = mem-channel-1 file-channel-2
# set channels for source
agent_foo.sources.avro-AppSrv-source1.channels = mem-channel-1 file-channel-2
# set channel for sinks
agent_foo.sinks.hdfs-Cluster1-sink1.channel = mem-channel-1
agent_foo.sinks.avro-forward-sink2.channel = file-channel-2
# channel selector configuration
agent_foo.sources.avro-AppSrv-source1.selector.type = multiplexing
agent_foo.sources.avro-AppSrv-source1.selector.header = State
agent_foo.sources.avro-AppSrv-source1.selector.mapping.CA = mem-channel-1
agent_foo.sources.avro-AppSrv-source1.selector.mapping.AZ = file-channel-2
agent_foo.sources.avro-AppSrv-source1.selector.mapping.NY = mem-channel-1 file-channel-2
agent_foo.sources.avro-AppSrv-source1.selector.default = mem-channel-1
The selector checks for a header called “State”. If the value is “CA” then its
sent to mem-channel-1, if its “AZ” then it goes to file-channel-2 or if its
“NY” then both. If the “State” header is not set or doesn’t match any of the
three, then it goes to mem-channel-1 which is designated as ‘default’.
The selector also supports optional channels. To specify optional channels for
a header, the config parameter ‘optional’ is used in the following way:
# channel selector configuration
agent_foo.sources.avro-AppSrv-source1.selector.type = multiplexing
agent_foo.sources.avro-AppSrv-source1.selector.header = State
agent_foo.sources.avro-AppSrv-source1.selector.mapping.CA = mem-channel-1
agent_foo.sources.avro-AppSrv-source1.selector.mapping.AZ = file-channel-2
agent_foo.sources.avro-AppSrv-source1.selector.mapping.NY = mem-channel-1 file-channel-2
agent_foo.sources.avro-AppSrv-source1.selector.optional.CA = mem-channel-1 file-channel-2
agent_foo.sources.avro-AppSrv-source1.selector.mapping.AZ = file-channel-2
agent_foo.sources.avro-AppSrv-source1.selector.default = mem-channel-1
The selector will attempt to write to the required channels first and will fail
the transaction if even one of these channels fails to consume the events. The
transaction is reattempted on all of the channels. Once all required
channels have consumed the events, then the selector will attempt to write to
the optional channels. A failure by any of the optional channels to consume the
event is simply ignored and not retried.
If there is an overlap between the optional channels and required channels for a
specific header, the channel is considered to be required, and a failure in the
channel will cause the entire set of required channels to be retried. For
instance, in the above example, for the header “CA” mem-channel-1 is considered
to be a required channel even though it is marked both as required and optional,
and a failure to write to this channel will cause that
event to be retried on all channels configured for the selector.
Note that if a header does not have any required channels, then the event will
be written to the default channels and will be attempted to be written to the
optional channels for that header. Specifying optional channels will still cause
the event to be written to the default channels, if no required channels are
specified. If no channels are designated as default and there are no required,
the selector will attempt to write the events to the optional channels. Any
failures are simply ignored in that case.
Flume Sources
Avro Source
Listens on Avro port and receives events from external Avro client streams.
When paired with the built-in Avro Sink on another (previous hop) Flume agent,
it can create tiered collection topologies.
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| channels |
– |
|
| type |
– |
The component type name, needs to be avro |
| bind |
– |
hostname or IP address to listen on |
| port |
– |
Port # to bind to |
| threads |
– |
Maximum number of worker threads to spawn |
| selector.type |
|
|
| selector.* |
|
|
| interceptors |
– |
Space-separated list of interceptors |
| interceptors.* |
|
|
| compression-type |
none |
This can be “none” or “deflate”. The compression-type must match the compression-type of matching AvroSource |
| ssl |
false |
Set this to true to enable SSL encryption. You must also specify a “keystore” and a “keystore-password”. |
| keystore |
– |
This is the path to a Java keystore file. Required for SSL. |
| keystore-type |
JKS |
The type of the Java keystore. This can be “JKS” or “PKCS12”. |
| keystore-password |
– |
The password for the Java keystore. Either this or the keystore-password-file setting is required for SSL. |
| keystore-password-file |
– |
The location of the file which stores the password to the keystore. Either this or the keystore-password setting is required for SSL. |
| keystore-password-file-type |
TEXT |
Format of the password file. This can be “AES” if password file was created using “flue-ng password” command. “TEXT” indicates the password is in clear text. |
| exclude-protocols |
SSLv3 |
Space-separated list of SSL/TLS protocols to exclude. SSLv3 will always be excluded in addition to the protocols specified. |
| ipFilter |
false |
Set this to true to enable ipFiltering for netty |
| ipFilter.rules |
– |
Define N netty ipFilter pattern rules with this config. |
Example for agent named a1:
a1.sources = r1
a1.channels = c1
a1.sources.r1.type = avro
a1.sources.r1.channels = c1
a1.sources.r1.bind = 0.0.0.0
a1.sources.r1.port = 4141
Example of ipFilter.rules
ipFilter.rules defines N netty ipFilters separated by a comma a pattern rule must be in this format.
<’allow’ or deny>:<’ip’ or ‘name’ for computer name>:<pattern>
or
allow/deny:ip/name:pattern
example: ipFilter.rules=allow:ip:127.*,allow:name:localhost,deny:ip:*
Note that the first rule to match will apply as the example below shows from a client on the localhost
This will Allow the client on localhost be deny clients from any other ip “allow:name:localhost,deny:ip:”
This will deny the client on localhost be allow clients from any other ip “deny:name:localhost,allow:ip:“
Thrift Source
Listens on Thrift port and receives events from external Thrift client streams.
When paired with the built-in ThriftSink on another (previous hop) Flume agent,
it can create tiered collection topologies.
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| channels |
– |
|
| type |
– |
The component type name, needs to be thrift |
| bind |
– |
hostname or IP address to listen on |
| port |
– |
Port # to bind to |
| threads |
– |
Maximum number of worker threads to spawn |
| selector.type |
|
|
| selector.* |
|
|
| interceptors |
– |
Space separated list of interceptors |
| interceptors.* |
|
|
Example for agent named a1:
a1.sources = r1
a1.channels = c1
a1.sources.r1.type = thrift
a1.sources.r1.channels = c1
a1.sources.r1.bind = 0.0.0.0
a1.sources.r1.port = 4141
Exec Source
Exec source runs a given Unix command on start-up and expects that process to
continuously produce data on standard out (stderr is simply discarded, unless
property logStdErr is set to true). If the process exits for any reason, the source also exits and
will produce no further data. This means configurations such as cat [named pipe]
or tail -F [file] are going to produce the desired results where as date
will probably not - the former two commands produce streams of data where as the
latter produces a single event and exits.
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| channels |
– |
|
| type |
– |
The component type name, needs to be exec |
| command |
– |
The command to execute |
| shell |
– |
A shell invocation used to run the command. e.g. /bin/sh -c. Required only for commands relying on shell features like wildcards, back ticks, pipes etc. |
| restartThrottle |
10000 |
Amount of time (in millis) to wait before attempting a restart |
| restart |
false |
Whether the executed cmd should be restarted if it dies |
| logStdErr |
false |
Whether the command’s stderr should be logged |
| batchSize |
20 |
The max number of lines to read and send to the channel at a time |
| selector.type |
replicating |
replicating or multiplexing |
| selector.* |
|
Depends on the selector.type value |
| interceptors |
– |
Space-separated list of interceptors |
| interceptors.* |
|
|
Warning
The problem with ExecSource and other asynchronous sources is that the
source can not guarantee that if there is a failure to put the event
into the Channel the client knows about it. In such cases, the data will
be lost. As a for instance, one of the most commonly requested features
is the tail -F [file]-like use case where an application writes
to a log file on disk and Flume tails the file, sending each line as an
event. While this is possible, there’s an obvious problem; what happens
if the channel fills up and Flume can’t send an event? Flume has no way
of indicating to the application writing the log file that it needs to
retain the log or that the event hasn’t been sent, for some reason. If
this doesn’t make sense, you need only know this: Your application can
never guarantee data has been received when using a unidirectional
asynchronous interface such as ExecSource! As an extension of this
warning - and to be completely clear - there is absolutely zero guarantee
of event delivery when using this source. For stronger reliability
guarantees, consider the Spooling Directory Source or direct integration
with Flume via the SDK.
Note
You can use ExecSource to emulate TailSource from Flume 0.9x (flume og).
Just use unix command tail -F /full/path/to/your/file. Parameter
-F is better in this case than -f as it will also follow file rotation.
Example for agent named a1:
a1.sources = r1
a1.channels = c1
a1.sources.r1.type = exec
a1.sources.r1.command = tail -F /var/log/secure
a1.sources.r1.channels = c1
The ‘shell’ config is used to invoke the ‘command’ through a command shell (such as Bash
or Powershell). The ‘command’ is passed as an argument to ‘shell’ for execution. This
allows the ‘command’ to use features from the shell such as wildcards, back ticks, pipes,
loops, conditionals etc. In the absence of the ‘shell’ config, the ‘command’ will be
invoked directly. Common values for ‘shell’ : ‘/bin/sh -c’, ‘/bin/ksh -c’,
‘cmd /c’, ‘powershell -Command’, etc.
agent_foo.sources.tailsource-1.type = exec
agent_foo.sources.tailsource-1.shell = /bin/bash -c
agent_foo.sources.tailsource-1.command = for i in /path/*.txt; do cat $i; done
JMS Source
JMS Source reads messages from a JMS destination such as a queue or topic. Being a JMS
application it should work with any JMS provider but has only been tested with ActiveMQ.
The JMS source provides configurable batch size, message selector, user/pass, and message
to flume event converter. Note that the vendor provided JMS jars should be included in the
Flume classpath using plugins.d directory (preferred), –classpath on command line, or
via FLUME_CLASSPATH variable in flume-env.sh.
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| channels |
– |
|
| type |
– |
The component type name, needs to be jms |
| initialContextFactory |
– |
Inital Context Factory, e.g: org.apache.activemq.jndi.ActiveMQInitialContextFactory |
| connectionFactory |
– |
The JNDI name the connection factory shoulld appear as |
| providerURL |
– |
The JMS provider URL |
| destinationName |
– |
Destination name |
| destinationType |
– |
Destination type (queue or topic) |
| messageSelector |
– |
Message selector to use when creating the consumer |
| userName |
– |
Username for the destination/provider |
| passwordFile |
– |
File containing the password for the destination/provider |
| passwordFileType |
TEXT |
Indicates how the password is stored in the passwordFile. Can also be set to “AES” if password file is created using “flume-ng password” command. “TEXT” indicates the password is in clear text. |
| batchSize |
100 |
Number of messages to consume in one batch |
| converter.type |
DEFAULT |
Class to use to convert messages to flume events. See below. |
| converter.* |
– |
Converter properties. |
| converter.charset |
UTF-8 |
Default converter only. Charset to use when converting JMS TextMessages to byte arrays. |
Converter
The JMS source allows pluggable converters, though it’s likely the default converter will work
for most purposes. The default converter is able to convert Bytes, Text, and Object messages
to FlumeEvents. In all cases, the properties in the message are added as headers to the
FlumeEvent.
- BytesMessage:
- Bytes of message are copied to body of the FlumeEvent. Cannot convert more than 2GB
of data per message.
- TextMessage:
- Text of message is converted to a byte array and copied to the body of the
FlumeEvent. The default converter uses UTF-8 by default but this is configurable.
- ObjectMessage:
- Object is written out to a ByteArrayOutputStream wrapped in an ObjectOutputStream and
the resulting array is copied to the body of the FlumeEvent.
Example for agent named a1:
a1.sources = r1
a1.channels = c1
a1.sources.r1.type = jms
a1.sources.r1.channels = c1
a1.sources.r1.initialContextFactory = org.apache.activemq.jndi.ActiveMQInitialContextFactory
a1.sources.r1.connectionFactory = GenericConnectionFactory
a1.sources.r1.providerURL = tcp://mqserver:61616
a1.sources.r1.destinationName = BUSINESS_DATA
a1.sources.r1.destinationType = QUEUE
Spooling Directory Source
This source lets you ingest data by placing files to be ingested into a
“spooling” directory on disk.
This source will watch the specified directory for new files, and will parse
events out of new files as they appear.
The event parsing logic is pluggable.
After a given file has been fully read
into the channel, it is renamed to indicate completion (or optionally deleted).
Unlike the Exec source, this source is reliable and will not miss data, even if
Flume is restarted or killed. In exchange for this reliability, only immutable,
uniquely-named files must be dropped into the spooling directory. Flume tries
to detect these problem conditions and will fail loudly if they are violated:
- If a file is written to after being placed into the spooling directory,
Flume will print an error to its log file and stop processing.
- If a file name is reused at a later time, Flume will print an error to its
log file and stop processing.
To avoid the above issues, it may be useful to add a unique identifier
(such as a timestamp) to log file names when they are moved into the spooling
directory.
Despite the reliability guarantees of this source, there are still
cases in which events may be duplicated if certain downstream failures occur.
This is consistent with the guarantees offered by other Flume components.
| Property Name |
Default |
Description |
|---|
| channels |
– |
|
| type |
– |
The component type name, needs to be spooldir. |
| spoolDir |
– |
The directory from which to read files from. |
| fileSuffix |
.COMPLETED |
Suffix to append to completely ingested files |
| deletePolicy |
never |
When to delete completed files: never or immediate |
| fileHeader |
false |
Whether to add a header storing the absolute path filename. |
| fileHeaderKey |
file |
Header key to use when appending absolute path filename to event header. |
| basenameHeader |
false |
Whether to add a header storing the basename of the file. |
| basenameHeaderKey |
basename |
Header Key to use when appending basename of file to event header. |
| ignorePattern |
^$ |
Regular expression specifying which files to ignore (skip) |
| trackerDir |
.flumespool |
Directory to store metadata related to processing of files.
If this path is not an absolute path, then it is interpreted as relative to the spoolDir. |
| consumeOrder |
oldest |
In which order files in the spooling directory will be consumed oldest,
youngest and random. In case of oldest and youngest, the last modified
time of the files will be used to compare the files. In case of a tie, the file
with smallest lexicographical order will be consumed first. In case of random any
file will be picked randomly. When using oldest and youngest the whole
directory will be scanned to pick the oldest/youngest file, which might be slow if there
are a large number of files, while using random may cause old files to be consumed
very late if new files keep coming in the spooling directory. |
| maxBackoff |
4000 |
The maximum time (in millis) to wait between consecutive attempts to write to the channel(s) if the channel is full. The source will start at a low backoff and increase it exponentially each time the channel throws a ChannelException, upto the value specified by this parameter. |
| batchSize |
100 |
Granularity at which to batch transfer to the channel |
| inputCharset |
UTF-8 |
Character set used by deserializers that treat the input file as text. |
| decodeErrorPolicy |
FAIL |
What to do when we see a non-decodable character in the input file.
FAIL: Throw an exception and fail to parse the file.
REPLACE: Replace the unparseable character with the “replacement character” char,
typically Unicode U+FFFD.
IGNORE: Drop the unparseable character sequence. |
| deserializer |
LINE |
Specify the deserializer used to parse the file into events.
Defaults to parsing each line as an event. The class specified must implement
EventDeserializer.Builder. |
| deserializer.* |
|
Varies per event deserializer. |
| bufferMaxLines |
– |
(Obselete) This option is now ignored. |
| bufferMaxLineLength |
5000 |
(Deprecated) Maximum length of a line in the commit buffer. Use deserializer.maxLineLength instead. |
| selector.type |
replicating |
replicating or multiplexing |
| selector.* |
|
Depends on the selector.type value |
| interceptors |
– |
Space-separated list of interceptors |
| interceptors.* |
|
|
Example for an agent named agent-1:
agent-1.channels = ch-1
agent-1.sources = src-1
agent-1.sources.src-1.type = spooldir
agent-1.sources.src-1.channels = ch-1
agent-1.sources.src-1.spoolDir = /var/log/apache/flumeSpool
agent-1.sources.src-1.fileHeader = true
Taildir Source
Note
This source is provided as a preview feature. It does not work on Windows. This source requires Java version 1.7 or later.
Watch the specified files, and tail them in nearly real-time once detected new lines appended to the each files.
If the new lines are being written, this source will retry reading them in wait for the completion of the write.
This source is reliable and will not miss data even when the tailing files rotate.
It periodically writes the last read position of each files on the given position file in JSON format.
If Flume is stopped or down for some reason, it can restart tailing from the position written on the existing position file.
In other use case, this source can also start tailing from the arbitrary position for each files using the given position file.
When there is no position file on the specified path, it will start tailing from the first line of each files by default.
Files will be consumed in order of their modification time. File with the oldest modification time will be consumed first.
This source does not rename or delete or do any modifications to the file being tailed.
Currently this source does not support tailing binary files. It reads text files line by line.
| Property Name |
Default |
Description |
|---|
| channels |
– |
|
| type |
– |
The component type name, needs to be TAILDIR. |
| filegroups |
– |
Space-separated list of file groups. Each file group indicates a set of files to be tailed. |
| filegroups.<filegroupName> |
– |
Absolute path of the file group. Regular expression (and not file system patterns) can be used for filename only. |
| positionFile |
~/.flume/taildir_position.json |
File in JSON format to record the inode, the absolute path and the last position of each tailing file. |
| headers.<filegroupName>.<headerKey> |
– |
Header value which is the set with header key. Multiple headers can be specified for one file group. |
| byteOffsetHeader |
false |
Whether to add the byte offset of a tailed line to a header called ‘byteoffset’. |
| skipToEnd |
false |
Whether to skip the position to EOF in the case of files not written on the position file. |
| idleTimeout |
120000 |
Time (ms) to close inactive files. If the closed file is appended new lines to, this source will automatically re-open it. |
| writePosInterval |
3000 |
Interval time (ms) to write the last position of each file on the position file. |
| batchSize |
100 |
Max number of lines to read and send to the channel at a time. Using the default is usually fine. |
| backoffSleepIncrement |
1000 |
The increment for time delay before reattempting to poll for new data, when the last attempt did not find any new data. |
| maxBackoffSleep |
5000 |
The max time delay between each reattempt to poll for new data, when the last attempt did not find any new data. |
Example for agent named a1:
a1.sources = r1
a1.channels = c1
a1.sources.r1.type = TAILDIR
a1.sources.r1.channels = c1
a1.sources.r1.positionFile = /var/log/flume/taildir_position.json
a1.sources.r1.filegroups = f1 f2
a1.sources.r1.filegroups.f1 = /var/log/test1/example.log
a1.sources.r1.headers.f1.headerKey1 = value1
a1.sources.r1.filegroups.f2 = /var/log/test2/.*log.*
a1.sources.r1.headers.f2.headerKey1 = value2
a1.sources.r1.headers.f2.headerKey2 = value2-2
Kafka Source
Kafka Source is an Apache Kafka consumer that reads messages from Kafka topics.
If you have multiple Kafka sources running, you can configure them with the same Consumer Group
so each will read a unique set of partitions for the topics.
| Property Name |
Default |
Description |
|---|
| channels |
– |
|
| type |
– |
The component type name, needs to be org.apache.flume.source.kafka.KafkaSource |
| kafka.bootstrap.servers |
– |
List of brokers in the Kafka cluster used by the source |
| kafka.consumer.group.id |
flume |
Unique identified of consumer group. Setting the same id in multiple sources or agents
indicates that they are part of the same consumer group |
| kafka.topics |
– |
Comma-separated list of topics the kafka consumer will read messages from. |
| kafka.topics.regex |
– |
Regex that defines set of topics the source is subscribed on. This property has higher priority
than kafka.topics and overrides kafka.topics if exists. |
| batchSize |
1000 |
Maximum number of messages written to Channel in one batch |
| batchDurationMillis |
1000 |
Maximum time (in ms) before a batch will be written to Channel
The batch will be written whenever the first of size and time will be reached. |
| useFlumeEventFormat |
false |
By default events are taken as bytes from the Kafka topic directly into the event body. Set to
true to read events as the Flume Avro binary format. Used in conjunction with the same property
on the KafkaSink or with the parseAsFlumeEvent property on the Kafka Channel this will preserve
any Flume headers sent on the producing side. |
| migrateZookeeperOffsets |
true |
When no Kafka stored offset is found, look up the offsets in Zookeeper and commit them to Kafka.
This should be true to support seamless Kafka client migration from older versions of Flume.
Once migrated this can be set to false, though that should generally not be required.
If no Zookeeper offset is found, the Kafka configuration kafka.consumer.auto.offset.reset
defines how offsets are handled. |
| Other Kafka Consumer Properties |
– |
These properties are used to configure the Kafka Consumer. Any producer property supported
by Kafka can be used. The only requirement is to prepend the property name with the prefix
kafka.consumer.
For example: kafka.consumer.auto.offset.reset
Check Kafka documentation for details |
Note
The Kafka Source overrides two Kafka consumer parameters:
auto.commit.enable is set to “false” by the source and every batch is committed. Kafka source guarantees at least once
strategy of messages retrieval. The duplicates can be present when the source starts.
The Kafka Source also provides defaults for the key.deserializer(org.apache.kafka.common.serialization.StringSerializer)
and value.deserializer(org.apache.kafka.common.serialization.ByteArraySerializer). Modification of these parameters is not recommended.
Deprecated Properties
| Property Name |
Default |
Description |
|---|
| topic |
– |
Use kafka.topics |
| groupId |
flume |
Use kafka.consumer.group.id |
| zookeeperConnect |
– |
Is no longer supported by kafka consumer client since 0.9.x. Use kafka.bootstrap.servers
to establish connection with kafka cluster |
Example for topic subscription by comma-separated topic list.
tier1.sources.source1.type = org.apache.flume.source.kafka.KafkaSource
tier1.sources.source1.channels = channel1
tier1.sources.source1.batchSize = 5000
tier1.sources.source1.batchDurationMillis = 2000
tier1.sources.source1.kafka.bootstrap.servers = localhost:9092
tier1.sources.source1.kafka.topics = test1, test2
tier1.sources.source1.kafka.consumer.group.id = custom.g.id
Example for topic subscription by regex
tier1.sources.source1.type = org.apache.flume.source.kafka.KafkaSource
tier1.sources.source1.channels = channel1
tier1.sources.source1.kafka.bootstrap.servers = localhost:9092
tier1.sources.source1.kafka.topics.regex = ^topic[0-9]$
# the default kafka.consumer.group.id=flume is used
NetCat Source
A netcat-like source that listens on a given port and turns each line of text
into an event. Acts like nc -k -l [host] [port]. In other words,
it opens a specified port and listens for data. The expectation is that the
supplied data is newline separated text. Each line of text is turned into a
Flume event and sent via the connected channel.
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| channels |
– |
|
| type |
– |
The component type name, needs to be netcat |
| bind |
– |
Host name or IP address to bind to |
| port |
– |
Port # to bind to |
| max-line-length |
512 |
Max line length per event body (in bytes) |
| ack-every-event |
true |
Respond with an “OK” for every event received |
| selector.type |
replicating |
replicating or multiplexing |
| selector.* |
|
Depends on the selector.type value |
| interceptors |
– |
Space-separated list of interceptors |
| interceptors.* |
|
|
Example for agent named a1:
a1.sources = r1
a1.channels = c1
a1.sources.r1.type = netcat
a1.sources.r1.bind = 0.0.0.0
a1.sources.r1.bind = 6666
a1.sources.r1.channels = c1
Sequence Generator Source
A simple sequence generator that continuously generates events with a counter
that starts from 0 and increments by 1. Useful mainly for testing.
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| channels |
– |
|
| type |
– |
The component type name, needs to be seq |
| selector.type |
|
replicating or multiplexing |
| selector.* |
replicating |
Depends on the selector.type value |
| interceptors |
– |
Space-separated list of interceptors |
| interceptors.* |
|
|
| batchSize |
1 |
|
Example for agent named a1:
a1.sources = r1
a1.channels = c1
a1.sources.r1.type = seq
a1.sources.r1.channels = c1
Syslog Sources
Reads syslog data and generate Flume events. The UDP source treats an entire
message as a single event. The TCP sources create a new event for each string
of characters separated by a newline (‘n’).
Required properties are in bold.
Syslog TCP Source
The original, tried-and-true syslog TCP source.
| Property Name |
Default |
Description |
|---|
| channels |
– |
|
| type |
– |
The component type name, needs to be syslogtcp |
| host |
– |
Host name or IP address to bind to |
| port |
– |
Port # to bind to |
| eventSize |
2500 |
Maximum size of a single event line, in bytes |
| keepFields |
false |
Setting this to true will preserve the Priority,
Timestamp and Hostname in the body of the event. |
| selector.type |
|
replicating or multiplexing |
| selector.* |
replicating |
Depends on the selector.type value |
| interceptors |
– |
Space-separated list of interceptors |
| interceptors.* |
|
|
For example, a syslog TCP source for agent named a1:
a1.sources = r1
a1.channels = c1
a1.sources.r1.type = syslogtcp
a1.sources.r1.port = 5140
a1.sources.r1.host = localhost
a1.sources.r1.channels = c1
Multiport Syslog TCP Source
This is a newer, faster, multi-port capable version of the Syslog TCP source.
Note that the ports configuration setting has replaced port.
Multi-port capability means that it can listen on many ports at once in an
efficient manner. This source uses the Apache Mina library to do that.
Provides support for RFC-3164 and many common RFC-5424 formatted messages.
Also provides the capability to configure the character set used on a per-port
basis.
| Property Name |
Default |
Description |
|---|
| channels |
– |
|
| type |
– |
The component type name, needs to be multiport_syslogtcp |
| host |
– |
Host name or IP address to bind to. |
| ports |
– |
Space-separated list (one or more) of ports to bind to. |
| eventSize |
2500 |
Maximum size of a single event line, in bytes. |
| keepFields |
false |
Setting this to true will preserve the
Priority, Timestamp and Hostname in the body of the event. |
| portHeader |
– |
If specified, the port number will be stored in the header of each event using the header name specified here. This allows for interceptors and channel selectors to customize routing logic based on the incoming port. |
| charset.default |
UTF-8 |
Default character set used while parsing syslog events into strings. |
| charset.port.<port> |
– |
Character set is configurable on a per-port basis. |
| batchSize |
100 |
Maximum number of events to attempt to process per request loop. Using the default is usually fine. |
| readBufferSize |
1024 |
Size of the internal Mina read buffer. Provided for performance tuning. Using the default is usually fine. |
| numProcessors |
(auto-detected) |
Number of processors available on the system for use while processing messages. Default is to auto-detect # of CPUs using the Java Runtime API. Mina will spawn 2 request-processing threads per detected CPU, which is often reasonable. |
| selector.type |
replicating |
replicating, multiplexing, or custom |
| selector.* |
– |
Depends on the selector.type value |
| interceptors |
– |
Space-separated list of interceptors. |
| interceptors.* |
|
|
For example, a multiport syslog TCP source for agent named a1:
a1.sources = r1
a1.channels = c1
a1.sources.r1.type = multiport_syslogtcp
a1.sources.r1.channels = c1
a1.sources.r1.host = 0.0.0.0
a1.sources.r1.ports = 10001 10002 10003
a1.sources.r1.portHeader = port
Syslog UDP Source
| Property Name |
Default |
Description |
|---|
| channels |
– |
|
| type |
– |
The component type name, needs to be syslogudp |
| host |
– |
Host name or IP address to bind to |
| port |
– |
Port # to bind to |
| keepFields |
false |
Setting this to true will preserve the Priority,
Timestamp and Hostname in the body of the event. |
| selector.type |
|
replicating or multiplexing |
| selector.* |
replicating |
Depends on the selector.type value |
| interceptors |
– |
Space-separated list of interceptors |
| interceptors.* |
|
|
For example, a syslog UDP source for agent named a1:
a1.sources = r1
a1.channels = c1
a1.sources.r1.type = syslogudp
a1.sources.r1.port = 5140
a1.sources.r1.host = localhost
a1.sources.r1.channels = c1
HTTP Source
A source which accepts Flume Events by HTTP POST and GET. GET should be used
for experimentation only. HTTP requests are converted into flume events by
a pluggable “handler” which must implement the HTTPSourceHandler interface.
This handler takes a HttpServletRequest and returns a list of
flume events. All events handled from one Http request are committed to the channel
in one transaction, thus allowing for increased efficiency on channels like
the file channel. If the handler throws an exception, this source will
return a HTTP status of 400. If the channel is full, or the source is unable to
append events to the channel, the source will return a HTTP 503 - Temporarily
unavailable status.
All events sent in one post request are considered to be one batch and
inserted into the channel in one transaction.
| Property Name |
Default |
Description |
|---|
| type |
|
The component type name, needs to be http |
| port |
– |
The port the source should bind to. |
| bind |
0.0.0.0 |
The hostname or IP address to listen on |
| handler |
org.apache.flume.source.http.JSONHandler |
The FQCN of the handler class. |
| handler.* |
– |
Config parameters for the handler |
| selector.type |
replicating |
replicating or multiplexing |
| selector.* |
|
Depends on the selector.type value |
| interceptors |
– |
Space-separated list of interceptors |
| interceptors.* |
|
|
| enableSSL |
false |
Set the property true, to enable SSL |
| excludeProtocols |
SSLv3 |
Space-separated list of SSL/TLS protocols to exclude. SSLv3 is always excluded. |
| keystore |
|
Location of the keystore includng keystore file name |
| keystorePassword |
|
Keystore password. Alternatively you can specify the password through a separate file using “keystorePasswordFile” setting |
| keystorePasswordFile |
– |
File containing the keystore password |
| keystorePasswordFileType |
TEXT |
Indicates how the password is stored in keystorePasswordFile. Can also be “AES” if the password file was created using “flume-ng password” command. “TEXT” indicates the password is in clear text. |
For example, a http source for agent named a1:
a1.sources = r1
a1.channels = c1
a1.sources.r1.type = http
a1.sources.r1.port = 5140
a1.sources.r1.channels = c1
a1.sources.r1.handler = org.example.rest.RestHandler
a1.sources.r1.handler.nickname = random props
JSON Handler
A handler is provided out of the box which can handle events represented in
JSON format, and supports UTF-8, UTF-16 and UTF-32 character sets. The handler
accepts an array of events (even if there is only one event, the event has to be
sent in an array) and converts them to a Flume event based on the
encoding specified in the request. If no encoding is specified, UTF-8 is assumed.
The JSON handler supports UTF-8, UTF-16 and UTF-32.
Events are represented as follows.
[{
"headers" : {
"timestamp" : "434324343",
"host" : "random_host.example.com"
},
"body" : "random_body"
},
{
"headers" : {
"namenode" : "namenode.example.com",
"datanode" : "random_datanode.example.com"
},
"body" : "really_random_body"
}]
To set the charset, the request must have content type specified as
application/json; charset=UTF-8 (replace UTF-8 with UTF-16 or UTF-32 as
required).
One way to create an event in the format expected by this handler is to
use JSONEvent provided in the Flume SDK and use Google Gson to create the JSON
string using the Gson#fromJson(Object, Type)
method. The type token to pass as the 2nd argument of this method
for list of events can be created by:
Type type = new TypeToken<List<JSONEvent>>() {}.getType();
Blob Handler
By default HTTPSource splits JSON input into Flume events. As an alternative, BlobHandler is a handler for HTTPSource that returns an event that contains the request parameters as well as the Binary Large Object (BLOB) uploaded with this request. For example a PDF or JPG file. Note that this approach is not suitable for very large objects because it buffers up the entire BLOB in RAM.
| Property Name |
Default |
Description |
|---|
| handler |
– |
The FQCN of this class: org.apache.flume.source.http.BlobHandler |
| handler.maxBlobLength |
100000000 |
The maximum number of bytes to read and buffer for a given request |
Legacy Sources
The legacy sources allow a Flume 1.x agent to receive events from Flume 0.9.4
agents. It accepts events in the Flume 0.9.4 format, converts them to the Flume
1.0 format, and stores them in the connected channel. The 0.9.4 event
properties like timestamp, pri, host, nanos, etc get converted to 1.x event
header attributes. The legacy source supports both Avro and Thrift RPC
connections. To use this bridge between two Flume versions, you need to start a
Flume 1.x agent with the avroLegacy or thriftLegacy source. The 0.9.4 agent
should have the agent Sink pointing to the host/port of the 1.x agent.
Note
The reliability semantics of Flume 1.x are different from that of
Flume 0.9.x. The E2E or DFO mode of a Flume 0.9.x agent will not be
supported by the legacy source. The only supported 0.9.x mode is the
best effort, though the reliability setting of the 1.x flow will be
applicable to the events once they are saved into the Flume 1.x
channel by the legacy source.
Required properties are in bold.
Avro Legacy Source
| Property Name |
Default |
Description |
|---|
| channels |
– |
|
| type |
– |
The component type name, needs to be org.apache.flume.source.avroLegacy.AvroLegacySource |
| host |
– |
The hostname or IP address to bind to |
| port |
– |
The port # to listen on |
| selector.type |
|
replicating or multiplexing |
| selector.* |
replicating |
Depends on the selector.type value |
| interceptors |
– |
Space-separated list of interceptors |
| interceptors.* |
|
|
Example for agent named a1:
a1.sources = r1
a1.channels = c1
a1.sources.r1.type = org.apache.flume.source.avroLegacy.AvroLegacySource
a1.sources.r1.host = 0.0.0.0
a1.sources.r1.bind = 6666
a1.sources.r1.channels = c1
Thrift Legacy Source
| Property Name |
Default |
Description |
|---|
| channels |
– |
|
| type |
– |
The component type name, needs to be org.apache.flume.source.thriftLegacy.ThriftLegacySource |
| host |
– |
The hostname or IP address to bind to |
| port |
– |
The port # to listen on |
| selector.type |
|
replicating or multiplexing |
| selector.* |
replicating |
Depends on the selector.type value |
| interceptors |
– |
Space-separated list of interceptors |
| interceptors.* |
|
|
Example for agent named a1:
a1.sources = r1
a1.channels = c1
a1.sources.r1.type = org.apache.flume.source.thriftLegacy.ThriftLegacySource
a1.sources.r1.host = 0.0.0.0
a1.sources.r1.bind = 6666
a1.sources.r1.channels = c1
Custom Source
A custom source is your own implementation of the Source interface. A custom
source’s class and its dependencies must be included in the agent’s classpath
when starting the Flume agent. The type of the custom source is its FQCN.
| Property Name |
Default |
Description |
|---|
| channels |
– |
|
| type |
– |
The component type name, needs to be your FQCN |
| selector.type |
|
replicating or multiplexing |
| selector.* |
replicating |
Depends on the selector.type value |
| interceptors |
– |
Space-separated list of interceptors |
| interceptors.* |
|
|
Example for agent named a1:
a1.sources = r1
a1.channels = c1
a1.sources.r1.type = org.example.MySource
a1.sources.r1.channels = c1
Scribe Source
Scribe is another type of ingest system. To adopt existing Scribe ingest system,
Flume should use ScribeSource based on Thrift with compatible transfering protocol.
For deployment of Scribe please follow the guide from Facebook.
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| type |
– |
The component type name, needs to be org.apache.flume.source.scribe.ScribeSource |
| port |
1499 |
Port that Scribe should be connected |
| workerThreads |
5 |
Handing threads number in Thrift |
| selector.type |
|
|
| selector.* |
|
|
Example for agent named a1:
a1.sources = r1
a1.channels = c1
a1.sources.r1.type = org.apache.flume.source.scribe.ScribeSource
a1.sources.r1.port = 1463
a1.sources.r1.workerThreads = 5
a1.sources.r1.channels = c1
Flume Sinks
HDFS Sink
This sink writes events into the Hadoop Distributed File System (HDFS). It
currently supports creating text and sequence files. It supports compression in
both file types. The files can be rolled (close current file and create a new
one) periodically based on the elapsed time or size of data or number of events.
It also buckets/partitions data by attributes like timestamp or machine
where the event originated. The HDFS directory path may contain formatting
escape sequences that will replaced by the HDFS sink to generate a
directory/file name to store the events. Using this sink requires hadoop to be
installed so that Flume can use the Hadoop jars to communicate with the HDFS
cluster. Note that a version of Hadoop that supports the sync() call is
required.
The following are the escape sequences supported:
| Alias |
Description |
|---|
| %{host} |
Substitute value of event header named “host”. Arbitrary header names are supported. |
| %t |
Unix time in milliseconds |
| %a |
locale’s short weekday name (Mon, Tue, ...) |
| %A |
locale’s full weekday name (Monday, Tuesday, ...) |
| %b |
locale’s short month name (Jan, Feb, ...) |
| %B |
locale’s long month name (January, February, ...) |
| %c |
locale’s date and time (Thu Mar 3 23:05:25 2005) |
| %d |
day of month (01) |
| %D |
date; same as %m/%d/%y |
| %H |
hour (00..23) |
| %I |
hour (01..12) |
| %j |
day of year (001..366) |
| %k |
hour ( 0..23) |
| %m |
month (01..12) |
| %M |
minute (00..59) |
| %p |
locale’s equivalent of am or pm |
| %s |
seconds since 1970-01-01 00:00:00 UTC |
| %S |
second (00..59) |
| %y |
last two digits of year (00..99) |
| %Y |
year (2010) |
| %z |
+hhmm numeric timezone (for example, -0400) |
The file in use will have the name mangled to include ”.tmp” at the end. Once
the file is closed, this extension is removed. This allows excluding partially
complete files in the directory.
Required properties are in bold.
Note
For all of the time related escape sequences, a header with the key
“timestamp” must exist among the headers of the event (unless hdfs.useLocalTimeStamp is set to true). One way to add
this automatically is to use the TimestampInterceptor.
| Name |
Default |
Description |
|---|
| channel |
– |
|
| type |
– |
The component type name, needs to be hdfs |
| hdfs.path |
– |
HDFS directory path (eg hdfs://namenode/flume/webdata/) |
| hdfs.filePrefix |
FlumeData |
Name prefixed to files created by Flume in hdfs directory |
| hdfs.fileSuffix |
– |
Suffix to append to file (eg .avro - NOTE: period is not automatically added) |
| hdfs.inUsePrefix |
– |
Prefix that is used for temporal files that flume actively writes into |
| hdfs.inUseSuffix |
.tmp |
Suffix that is used for temporal files that flume actively writes into |
| hdfs.rollInterval |
30 |
Number of seconds to wait before rolling current file
(0 = never roll based on time interval) |
| hdfs.rollSize |
1024 |
File size to trigger roll, in bytes (0: never roll based on file size) |
| hdfs.rollCount |
10 |
Number of events written to file before it rolled
(0 = never roll based on number of events) |
| hdfs.idleTimeout |
0 |
Timeout after which inactive files get closed
(0 = disable automatic closing of idle files) |
| hdfs.batchSize |
100 |
number of events written to file before it is flushed to HDFS |
| hdfs.codeC |
– |
Compression codec. one of following : gzip, bzip2, lzo, lzop, snappy |
| hdfs.fileType |
SequenceFile |
File format: currently SequenceFile, DataStream or CompressedStream
(1)DataStream will not compress output file and please don’t set codeC
(2)CompressedStream requires set hdfs.codeC with an available codeC |
| hdfs.maxOpenFiles |
5000 |
Allow only this number of open files. If this number is exceeded, the oldest file is closed. |
| hdfs.minBlockReplicas |
– |
Specify minimum number of replicas per HDFS block. If not specified, it comes from the default Hadoop config in the classpath. |
| hdfs.writeFormat |
– |
Format for sequence file records. One of “Text” or “Writable” (the default). |
| hdfs.callTimeout |
10000 |
Number of milliseconds allowed for HDFS operations, such as open, write, flush, close.
This number should be increased if many HDFS timeout operations are occurring. |
| hdfs.threadsPoolSize |
10 |
Number of threads per HDFS sink for HDFS IO ops (open, write, etc.) |
| hdfs.rollTimerPoolSize |
1 |
Number of threads per HDFS sink for scheduling timed file rolling |
| hdfs.kerberosPrincipal |
– |
Kerberos user principal for accessing secure HDFS |
| hdfs.kerberosKeytab |
– |
Kerberos keytab for accessing secure HDFS |
| hdfs.proxyUser |
|
|
| hdfs.round |
false |
Should the timestamp be rounded down (if true, affects all time based escape sequences except %t) |
| hdfs.roundValue |
1 |
Rounded down to the highest multiple of this (in the unit configured using hdfs.roundUnit), less than current time. |
| hdfs.roundUnit |
second |
The unit of the round down value - second, minute or hour. |
| hdfs.timeZone |
Local Time |
Name of the timezone that should be used for resolving the directory path, e.g. America/Los_Angeles. |
| hdfs.useLocalTimeStamp |
false |
Use the local time (instead of the timestamp from the event header) while replacing the escape sequences. |
| hdfs.closeTries |
0 |
Number of times the sink must try renaming a file, after initiating a close attempt. If set to 1, this sink will not re-try a failed rename
(due to, for example, NameNode or DataNode failure), and may leave the file in an open state with a .tmp extension.
If set to 0, the sink will try to rename the file until the file is eventually renamed (there is no limit on the number of times it would try).
The file may still remain open if the close call fails but the data will be intact and in this case, the file will be closed only after a Flume restart. |
| hdfs.retryInterval |
180 |
Time in seconds between consecutive attempts to close a file. Each close call costs multiple RPC round-trips to the Namenode,
so setting this too low can cause a lot of load on the name node. If set to 0 or less, the sink will not
attempt to close the file if the first attempt fails, and may leave the file open or with a ”.tmp” extension. |
| serializer |
TEXT |
Other possible options include avro_event or the
fully-qualified class name of an implementation of the
EventSerializer.Builder interface. |
| serializer.* |
|
|
Example for agent named a1:
a1.channels = c1
a1.sinks = k1
a1.sinks.k1.type = hdfs
a1.sinks.k1.channel = c1
a1.sinks.k1.hdfs.path = /flume/events/%y-%m-%d/%H%M/%S
a1.sinks.k1.hdfs.filePrefix = events-
a1.sinks.k1.hdfs.round = true
a1.sinks.k1.hdfs.roundValue = 10
a1.sinks.k1.hdfs.roundUnit = minute
The above configuration will round down the timestamp to the last 10th minute. For example, an event with
timestamp 11:54:34 AM, June 12, 2012 will cause the hdfs path to become /flume/events/2012-06-12/1150/00.
Hive Sink
This sink streams events containing delimited text or JSON data directly into a Hive table or partition.
Events are written using Hive transactions. As soon as a set of events are committed to Hive, they become
immediately visible to Hive queries. Partitions to which flume will stream to can either be pre-created
or, optionally, Flume can create them if they are missing. Fields from incoming event data are mapped to
corresponding columns in the Hive table.
| Name |
Default |
Description |
|---|
| channel |
– |
|
| type |
– |
The component type name, needs to be hive |
| hive.metastore |
– |
Hive metastore URI (eg thrift://a.b.com:9083 ) |
| hive.database |
– |
Hive database name |
| hive.table |
– |
Hive table name |
| hive.partition |
– |
Comma separate list of partition values identifying the partition to write to. May contain escape
sequences. E.g: If the table is partitioned by (continent: string, country :string, time : string)
then ‘Asia,India,2014-02-26-01-21’ will indicate continent=Asia,country=India,time=2014-02-26-01-21 |
| hive.kerberosPrincipal |
– |
Kerberos user principal for accessing secure Hive |
| hive.kerberosKeytab |
– |
Kerberos keytab for accessing secure Hive |
| hive.txnsPerBatchAsk |
100 |
Hive grants a batch of transactions instead of single transactions to streaming clients like Flume.
This setting configures the number of desired transactions per Transaction Batch. Data from all
transactions in a single batch end up in a single file. Flume will write a maximum of batchSize events
in each transaction in the batch. This setting in conjunction with batchSize provides control over the
size of each file. Note that eventually Hive will transparently compact these files into larger files. |
| heartBeatInterval |
240 |
(In seconds) Interval between consecutive heartbeats sent to Hive to keep unused transactions from expiring.
Set this value to 0 to disable heartbeats. |
| autoCreatePartitions |
true |
Flume will automatically create the necessary Hive partitions to stream to |
| batchSize |
15000 |
Max number of events written to Hive in a single Hive transaction |
| maxOpenConnections |
500 |
Allow only this number of open connections. If this number is exceeded, the least recently used connection is closed. |
| callTimeout |
10000 |
(In milliseconds) Timeout for Hive & HDFS I/O operations, such as openTxn, write, commit, abort. |
| serializer |
|
Serializer is responsible for parsing out field from the event and mapping them to columns in the hive table.
Choice of serializer depends upon the format of the data in the event. Supported serializers: DELIMITED and JSON |
| roundUnit |
minute |
The unit of the round down value - second, minute or hour. |
| roundValue |
1 |
Rounded down to the highest multiple of this (in the unit configured using hive.roundUnit), less than current time |
| timeZone |
Local Time |
Name of the timezone that should be used for resolving the escape sequences in partition, e.g. America/Los_Angeles. |
| useLocalTimeStamp |
false |
Use the local time (instead of the timestamp from the event header) while replacing the escape sequences. |
Following serializers are provided for Hive sink:
JSON: Handles UTF8 encoded Json (strict syntax) events and requires no configration. Object names
in the JSON are mapped directly to columns with the same name in the Hive table.
Internally uses org.apache.hive.hcatalog.data.JsonSerDe but is independent of the Serde of the Hive table.
This serializer requires HCatalog to be installed.
DELIMITED: Handles simple delimited textual events.
Internally uses LazySimpleSerde but is independent of the Serde of the Hive table.
| Name |
Default |
Description |
|---|
| serializer.delimiter |
, |
(Type: string) The field delimiter in the incoming data. To use special
characters, surround them with double quotes like “\t” |
| serializer.fieldnames |
– |
The mapping from input fields to columns in hive table. Specified as a
comma separated list (no spaces) of hive table columns names, identifying
the input fields in order of their occurrence. To skip fields leave the
column name unspecified. Eg. ‘time,,ip,message’ indicates the 1st, 3rd
and 4th fields in input map to time, ip and message columns in the hive table. |
| serializer.serdeSeparator |
Ctrl-A |
(Type: character) Customizes the separator used by underlying serde. There
can be a gain in efficiency if the fields in serializer.fieldnames are in
same order as table columns, the serializer.delimiter is same as the
serializer.serdeSeparator and number of fields in serializer.fieldnames
is less than or equal to number of table columns, as the fields in incoming
event body do not need to be reordered to match order of table columns.
Use single quotes for special characters like ‘\t’.
Ensure input fields do not contain this character. NOTE: If serializer.delimiter
is a single character, preferably set this to the same character |
The following are the escape sequences supported:
| Alias |
Description |
|---|
| %{host} |
Substitute value of event header named “host”. Arbitrary header names are supported. |
| %t |
Unix time in milliseconds |
| %a |
locale’s short weekday name (Mon, Tue, ...) |
| %A |
locale’s full weekday name (Monday, Tuesday, ...) |
| %b |
locale’s short month name (Jan, Feb, ...) |
| %B |
locale’s long month name (January, February, ...) |
| %c |
locale’s date and time (Thu Mar 3 23:05:25 2005) |
| %d |
day of month (01) |
| %D |
date; same as %m/%d/%y |
| %H |
hour (00..23) |
| %I |
hour (01..12) |
| %j |
day of year (001..366) |
| %k |
hour ( 0..23) |
| %m |
month (01..12) |
| %M |
minute (00..59) |
| %p |
locale’s equivalent of am or pm |
| %s |
seconds since 1970-01-01 00:00:00 UTC |
| %S |
second (00..59) |
| %y |
last two digits of year (00..99) |
| %Y |
year (2010) |
| %z |
+hhmm numeric timezone (for example, -0400) |
Note
For all of the time related escape sequences, a header with the key
“timestamp” must exist among the headers of the event (unless useLocalTimeStamp is set to true). One way to add
this automatically is to use the TimestampInterceptor.
Example Hive table :
create table weblogs ( id int , msg string )
partitioned by (continent string, country string, time string)
clustered by (id) into 5 buckets
stored as orc;
Example for agent named a1:
a1.channels = c1
a1.channels.c1.type = memory
a1.sinks = k1
a1.sinks.k1.type = hive
a1.sinks.k1.channel = c1
a1.sinks.k1.hive.metastore = thrift://127.0.0.1:9083
a1.sinks.k1.hive.database = logsdb
a1.sinks.k1.hive.table = weblogs
a1.sinks.k1.hive.partition = asia,%{country},%y-%m-%d-%H-%M
a1.sinks.k1.useLocalTimeStamp = false
a1.sinks.k1.round = true
a1.sinks.k1.roundValue = 10
a1.sinks.k1.roundUnit = minute
a1.sinks.k1.serializer = DELIMITED
a1.sinks.k1.serializer.delimiter = "\t"
a1.sinks.k1.serializer.serdeSeparator = '\t'
a1.sinks.k1.serializer.fieldnames =id,,msg
The above configuration will round down the timestamp to the last 10th minute. For example, an event with
timestamp header set to 11:54:34 AM, June 12, 2012 and ‘country’ header set to ‘india’ will evaluate to the
partition (continent=’asia’,country=’india’,time=‘2012-06-12-11-50’. The serializer is configured to
accept tab separated input containing three fields and to skip the second field.
Logger Sink
Logs event at INFO level. Typically useful for testing/debugging purpose. Required properties are
in bold. This sink is the only exception which doesn’t require the extra configuration
explained in the Logging raw data section.
| Property Name |
Default |
Description |
|---|
| channel |
– |
|
| type |
– |
The component type name, needs to be logger |
Example for agent named a1:
a1.channels = c1
a1.sinks = k1
a1.sinks.k1.type = logger
a1.sinks.k1.channel = c1
Avro Sink
This sink forms one half of Flume’s tiered collection support. Flume events
sent to this sink are turned into Avro events and sent to the configured
hostname / port pair. The events are taken from the configured Channel in
batches of the configured batch size.
Required properties are in bold.
| Property Name |
Default Description |
|
|---|
| channel |
– |
|
| type |
– |
The component type name, needs to be avro. |
| hostname |
– |
The hostname or IP address to bind to. |
| port |
– |
The port # to listen on. |
| batch-size |
100 |
number of event to batch together for send. |
| connect-timeout |
20000 |
Amount of time (ms) to allow for the first (handshake) request. |
| request-timeout |
20000 |
Amount of time (ms) to allow for requests after the first. |
| reset-connection-interval |
none |
Amount of time (s) before the connection to the next hop is reset. This will force the Avro Sink to reconnect to the next hop. This will allow the sink to connect to hosts behind a hardware load-balancer when news hosts are added without having to restart the agent. |
| compression-type |
none |
This can be “none” or “deflate”. The compression-type must match the compression-type of matching AvroSource |
| compression-level |
6 |
The level of compression to compress event. 0 = no compression and 1-9 is compression. The higher the number the more compression |
| ssl |
false |
Set to true to enable SSL for this AvroSink. When configuring SSL, you can optionally set a “truststore”, “truststore-password”, “truststore-type”, and specify whether to “trust-all-certs”. |
| trust-all-certs |
false |
If this is set to true, SSL server certificates for remote servers (Avro Sources) will not be checked. This should NOT be used in production because it makes it easier for an attacker to execute a man-in-the-middle attack and “listen in” on the encrypted connection. |
| truststore |
– |
The path to a custom Java truststore file. Flume uses the certificate authority information in this file to determine whether the remote Avro Source’s SSL authentication credentials should be trusted. If not specified, the default Java JSSE certificate authority files (typically “jssecacerts” or “cacerts” in the Oracle JRE) will be used. |
| truststore-password |
– |
The password for the specified truststore. Alternatively you can set the password in an external file using the “truststore-password-file” setting. |
| truststore-password-file |
– |
File in which password for the truststore is stored. |
| truststore-password-file-type |
TEXT |
Type of password-file. Can also be “AES” if the file is created using “flume-ng password” command. “TEXT” indicates the password is in clear text. |
| truststore-type |
JKS |
The type of the Java truststore. This can be “JKS” or other supported Java truststore type. |
| exclude-protocols |
SSLv2Hello SSLv3 |
Space-separated list of SSL/TLS protocols to exclude |
| maxIoWorkers |
2 * the number of available processors in the machine |
The maximum number of I/O worker threads. This is configured on the NettyAvroRpcClient NioClientSocketChannelFactory. |
Example for agent named a1:
a1.channels = c1
a1.sinks = k1
a1.sinks.k1.type = avro
a1.sinks.k1.channel = c1
a1.sinks.k1.hostname = 10.10.10.10
a1.sinks.k1.port = 4545
Thrift Sink
This sink forms one half of Flume’s tiered collection support. Flume events
sent to this sink are turned into Thrift events and sent to the configured
hostname / port pair. The events are taken from the configured Channel in
batches of the configured batch size.
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| channel |
– |
|
| type |
– |
The component type name, needs to be thrift. |
| hostname |
– |
The hostname or IP address to bind to. |
| port |
– |
The port # to listen on. |
| batch-size |
100 |
number of event to batch together for send. |
| connect-timeout |
20000 |
Amount of time (ms) to allow for the first (handshake) request. |
| request-timeout |
20000 |
Amount of time (ms) to allow for requests after the first. |
| connection-reset-interval |
none |
Amount of time (s) before the connection to the next hop is reset. This will force the Thrift Sink to reconnect to the next hop. This will allow the sink to connect to hosts behind a hardware load-balancer when news hosts are added without having to restart the agent. |
Example for agent named a1:
a1.channels = c1
a1.sinks = k1
a1.sinks.k1.type = thrift
a1.sinks.k1.channel = c1
a1.sinks.k1.hostname = 10.10.10.10
a1.sinks.k1.port = 4545
IRC Sink
The IRC sink takes messages from attached channel and relays those to
configured IRC destinations.
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| channel |
– |
|
| type |
– |
The component type name, needs to be irc |
| hostname |
– |
The hostname or IP address to connect to |
| port |
6667 |
The port number of remote host to connect |
| nick |
– |
Nick name |
| user |
– |
User name |
| password |
– |
User password |
| chan |
– |
channel |
| name |
|
|
| splitlines |
– |
(boolean) |
| splitchars |
n |
line separator (if you were to enter the default value
into the config file, then you would need to escape the
backslash, like this: “\n”) |
Example for agent named a1:
a1.channels = c1
a1.sinks = k1
a1.sinks.k1.type = irc
a1.sinks.k1.channel = c1
a1.sinks.k1.hostname = irc.yourdomain.com
a1.sinks.k1.nick = flume
a1.sinks.k1.chan = #flume
File Roll Sink
Stores events on the local filesystem.
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| channel |
– |
|
| type |
– |
The component type name, needs to be file_roll. |
| sink.directory |
– |
The directory where files will be stored |
| sink.rollInterval |
30 |
Roll the file every 30 seconds. Specifying 0 will disable rolling and cause all events to be written to a single file. |
| sink.serializer |
TEXT |
Other possible options include avro_event or the FQCN of an implementation of EventSerializer.Builder interface. |
| batchSize |
100 |
|
Example for agent named a1:
a1.channels = c1
a1.sinks = k1
a1.sinks.k1.type = file_roll
a1.sinks.k1.channel = c1
a1.sinks.k1.sink.directory = /var/log/flume
Null Sink
Discards all events it receives from the channel.
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| channel |
– |
|
| type |
– |
The component type name, needs to be null. |
| batchSize |
100 |
|
Example for agent named a1:
a1.channels = c1
a1.sinks = k1
a1.sinks.k1.type = null
a1.sinks.k1.channel = c1
HBase Sinks
HBase Sink
This sink writes data to HBase. The Hbase configuration is picked up from the first
hbase-site.xml encountered in the classpath. A class implementing HbaseEventSerializer
which is specified by the configuration is used to convert the events into
HBase puts and/or increments. These puts and increments are then written
to HBase. This sink provides the same consistency guarantees as HBase,
which is currently row-wise atomicity. In the event of Hbase failing to
write certain events, the sink will replay all events in that transaction.
The HBaseSink supports writing data to secure HBase. To write to secure HBase, the user
the agent is running as must have write permissions to the table the sink is configured
to write to. The principal and keytab to use to authenticate against the KDC can be specified
in the configuration. The hbase-site.xml in the Flume agent’s classpath
must have authentication set to kerberos (For details on how to do this, please refer to
HBase documentation).
For convenience, two serializers are provided with Flume. The
SimpleHbaseEventSerializer (org.apache.flume.sink.hbase.SimpleHbaseEventSerializer)
writes the event body
as-is to HBase, and optionally increments a column in Hbase. This is primarily
an example implementation. The RegexHbaseEventSerializer
(org.apache.flume.sink.hbase.RegexHbaseEventSerializer) breaks the event body
based on the given regex and writes each part into different columns.
The type is the FQCN: org.apache.flume.sink.hbase.HBaseSink.
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| channel |
– |
|
| type |
– |
The component type name, needs to be hbase |
| table |
– |
The name of the table in Hbase to write to. |
| columnFamily |
– |
The column family in Hbase to write to. |
| zookeeperQuorum |
– |
The quorum spec. This is the value for the property hbase.zookeeper.quorum in hbase-site.xml |
| znodeParent |
/hbase |
The base path for the znode for the -ROOT- region. Value of zookeeper.znode.parent in hbase-site.xml |
| batchSize |
100 |
Number of events to be written per txn. |
| coalesceIncrements |
false |
Should the sink coalesce multiple increments to a cell per batch. This might give
better performance if there are multiple increments to a limited number of cells. |
| serializer |
org.apache.flume.sink.hbase.SimpleHbaseEventSerializer |
Default increment column = “iCol”, payload column = “pCol”. |
| serializer.* |
– |
Properties to be passed to the serializer. |
| kerberosPrincipal |
– |
Kerberos user principal for accessing secure HBase |
| kerberosKeytab |
– |
Kerberos keytab for accessing secure HBase |
Example for agent named a1:
a1.channels = c1
a1.sinks = k1
a1.sinks.k1.type = hbase
a1.sinks.k1.table = foo_table
a1.sinks.k1.columnFamily = bar_cf
a1.sinks.k1.serializer = org.apache.flume.sink.hbase.RegexHbaseEventSerializer
a1.sinks.k1.channel = c1
Async HBase Sink
This sink writes data to HBase using an asynchronous model. A class implementing
AsyncHbaseEventSerializer which is specified by the configuration is used to convert the events into
HBase puts and/or increments. These puts and increments are then written
to HBase. This sink uses the Asynchbase API to write to
HBase. This sink provides the same consistency guarantees as HBase,
which is currently row-wise atomicity. In the event of Hbase failing to
write certain events, the sink will replay all events in that transaction.
The type is the FQCN: org.apache.flume.sink.hbase.AsyncHBaseSink.
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| channel |
– |
|
| type |
– |
The component type name, needs to be asynchbase |
| table |
– |
The name of the table in Hbase to write to. |
| zookeeperQuorum |
– |
The quorum spec. This is the value for the property hbase.zookeeper.quorum in hbase-site.xml |
| znodeParent |
/hbase |
The base path for the znode for the -ROOT- region. Value of zookeeper.znode.parent in hbase-site.xml |
| columnFamily |
– |
The column family in Hbase to write to. |
| batchSize |
100 |
Number of events to be written per txn. |
| coalesceIncrements |
false |
Should the sink coalesce multiple increments to a cell per batch. This might give
better performance if there are multiple increments to a limited number of cells. |
| timeout |
60000 |
The length of time (in milliseconds) the sink waits for acks from hbase for
all events in a transaction. |
| serializer |
org.apache.flume.sink.hbase.SimpleAsyncHbaseEventSerializer |
|
| serializer.* |
– |
Properties to be passed to the serializer. |
Note that this sink takes the Zookeeper Quorum and parent znode information in
the configuration. Zookeeper Quorum and parent node configuration may be
specified in the flume configuration file. Alternatively, these configuration
values are taken from the first hbase-site.xml file in the classpath.
If these are not provided in the configuration, then the sink
will read this information from the first hbase-site.xml file in the classpath.
Example for agent named a1:
a1.channels = c1
a1.sinks = k1
a1.sinks.k1.type = asynchbase
a1.sinks.k1.table = foo_table
a1.sinks.k1.columnFamily = bar_cf
a1.sinks.k1.serializer = org.apache.flume.sink.hbase.SimpleAsyncHbaseEventSerializer
a1.sinks.k1.channel = c1
Morphline Solr Sink
This sink extracts data from Flume events, transforms it, and loads it in near-real-time into Apache Solr servers, which in turn serve queries to end users or search applications.
This sink is well suited for use cases that stream raw data into HDFS (via the HdfsSink) and simultaneously extract, transform and load the same data into Solr (via MorphlineSolrSink). In particular, this sink can process arbitrary heterogeneous raw data from disparate data sources and turn it into a data model that is useful to Search applications.
The ETL functionality is customizable using a morphline configuration file that defines a chain of transformation commands that pipe event records from one command to another.
Morphlines can be seen as an evolution of Unix pipelines where the data model is generalized to work with streams of generic records, including arbitrary binary payloads. A morphline command is a bit like a Flume Interceptor. Morphlines can be embedded into Hadoop components such as Flume.
Commands to parse and transform a set of standard data formats such as log files, Avro, CSV, Text, HTML, XML, PDF, Word, Excel, etc. are provided out of the box, and additional custom commands and parsers for additional data formats can be added as morphline plugins. Any kind of data format can be indexed and any Solr documents for any kind of Solr schema can be generated, and any custom ETL logic can be registered and executed.
Morphlines manipulate continuous streams of records. The data model can be described as follows: A record is a set of named fields where each field has an ordered list of one or more values. A value can be any Java Object. That is, a record is essentially a hash table where each hash table entry contains a String key and a list of Java Objects as values. (The implementation uses Guava’s ArrayListMultimap, which is a ListMultimap). Note that a field can have multiple values and any two records need not use common field names.
This sink fills the body of the Flume event into the _attachment_body field of the morphline record, as well as copies the headers of the Flume event into record fields of the same name. The commands can then act on this data.
Routing to a SolrCloud cluster is supported to improve scalability. Indexing load can be spread across a large number of MorphlineSolrSinks for improved scalability. Indexing load can be replicated across multiple MorphlineSolrSinks for high availability, for example using Flume features such as Load balancing Sink Processor. MorphlineInterceptor can also help to implement dynamic routing to multiple Solr collections (e.g. for multi-tenancy).
The morphline and solr jars required for your environment must be placed in the lib directory of the Apache Flume installation.
The type is the FQCN: org.apache.flume.sink.solr.morphline.MorphlineSolrSink
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| channel |
– |
|
| type |
– |
The component type name, needs to be morphlinesolr |
| morphlineFile |
– |
The relative or absolute path on the local file system to the morphline configuration file. Example: /etc/flume-ng/conf/morphline.conf |
| morphlineId |
null |
Optional name used to identify a morphline if there are multiple morphlines in a morphline config file |
| batchSize |
1000 |
The maximum number of events to take per flume transaction. |
| batchDurationMillis |
1000 |
The maximum duration per flume transaction (ms). The transaction commits after this duration or when batchSize is exceeded, whichever comes first. |
| handlerClass |
org.apache.flume.sink.solr.morphline.MorphlineHandlerImpl |
The FQCN of a class implementing org.apache.flume.sink.solr.morphline.MorphlineHandler |
Example for agent named a1:
a1.channels = c1
a1.sinks = k1
a1.sinks.k1.type = morphlinesolr
a1.sinks.k1.channel = c1
a1.sinks.k1.morphlineFile = /etc/flume-ng/conf/morphline.conf
# a1.sinks.k1.morphlineId = morphline1
# a1.sinks.k1.batchSize = 1000
# a1.sinks.k1.batchDurationMillis = 1000
Elasticsearch Sink
This sink writes data to an elasticsearch cluster. By default, events will be written so that the Kibana graphical interface
can display them - just as if logstash wrote them.
The elasticsearch and lucene-core jars required for your environment must be placed in the lib directory of the Apache Flume installation.
Elasticsearch requires that the major version of the client JAR match that of the server and that both are running the same minor version
of the JVM. SerializationExceptions will appear if this is incorrect. To select the required version first determine the version of
elasticsearch and the JVM version the target cluster is running. Then select an elasticsearch client library which matches the major version.
A 0.19.x client can talk to a 0.19.x cluster; 0.20.x can talk to 0.20.x and 0.90.x can talk to 0.90.x. Once the elasticsearch version has
been determined then read the pom.xml file to determine the correct lucene-core JAR version to use. The Flume agent which is running
the ElasticSearchSink should also match the JVM the target cluster is running down to the minor version.
Events will be written to a new index every day. The name will be <indexName>-yyyy-MM-dd where <indexName> is the indexName parameter. The sink
will start writing to a new index at midnight UTC.
Events are serialized for elasticsearch by the ElasticSearchLogStashEventSerializer by default. This behaviour can be overridden with
the serializer parameter. This parameter accepts implementations of org.apache.flume.sink.elasticsearch.ElasticSearchEventSerializer
or org.apache.flume.sink.elasticsearch.ElasticSearchIndexRequestBuilderFactory. Implementing ElasticSearchEventSerializer is deprecated in favour of
the more powerful ElasticSearchIndexRequestBuilderFactory.
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| channel |
– |
|
| type |
– |
The component type name needs to be ‘elasticsearch’ |
| hostNames |
– |
Comma separated list of hostname:port, if the port is not present the default port ‘9300’ will be used |
| indexName |
flume |
The name of the index which the date will be appended to. Example ‘flume’ -> ‘flume-yyyy-MM-dd’ |
| indexType |
logs |
The type to index the document to, defaults to ‘log’ |
| clusterName |
elasticsearch |
Name of the ElasticSearch cluster to connect to |
| batchSize |
100 |
Number of events to be written per txn. |
| ttl |
– |
TTL in days, when set will cause the expired documents to be deleted automatically,
if not set documents will never be automatically deleted. TTL is accepted both in the earlier form of
integer only e.g. a1.sinks.k1.ttl = 5 and also with a qualifier ms (millisecond), s (second), m (minute),
h (hour), d (day) and w (week). Example a1.sinks.k1.ttl = 5d will set TTL to 5 days. Follow
https://www.elastic.co/guide/en/elasticsearch/reference/2.0/mapping-ttl-field.html for more information. |
| serializer |
org.apache.flume.sink.elasticsearch.ElasticSearchLogStashEventSerializer |
The ElasticSearchIndexRequestBuilderFactory or ElasticSearchEventSerializer to use. Implementations of
either class are accepted but ElasticSearchIndexRequestBuilderFactory is preferred. |
| serializer.* |
– |
Properties to be passed to the serializer. |
Example for agent named a1:
a1.channels = c1
a1.sinks = k1
a1.sinks.k1.type = elasticsearch
a1.sinks.k1.hostNames = 127.0.0.1:9200,127.0.0.2:9300
a1.sinks.k1.indexName = foo_index
a1.sinks.k1.indexType = bar_type
a1.sinks.k1.clusterName = foobar_cluster
a1.sinks.k1.batchSize = 500
a1.sinks.k1.ttl = 5d
a1.sinks.k1.serializer = org.apache.flume.sink.elasticsearch.ElasticSearchDynamicSerializer
a1.sinks.k1.channel = c1
Kite Dataset Sink (experimental)
Warning
This source is experimental and may change between minor versions of Flume.
Use at your own risk.
Experimental sink that writes events to a Kite Dataset.
This sink will deserialize the body of each incoming event and store the
resulting record in a Kite Dataset. It determines target Dataset by opening a
repository URI, kite.repo.uri, and loading a Dataset by name,
kite.dataset.name.
The only supported serialization is avro, and the record schema must be passed
in the event headers, using either flume.avro.schema.literal with the JSON
schema representation or flume.avro.schema.url with a URL where the schema
may be found (hdfs:/... URIs are supported). This is compatible with the
Log4jAppender flume client and the spooling directory source’s Avro
deserializer using deserializer.schemaType = LITERAL.
Note 1: The flume.avro.schema.hash header is not supported.
Note 2: In some cases, file rolling may occur slightly after the roll interval
has been exceeded. However, this delay will not exceed 5 seconds. In most
cases, the delay is neglegible.
| Property Name |
Default |
Description |
|---|
| channel |
– |
|
| type |
– |
Must be org.apache.flume.sink.kite.DatasetSink |
| kite.repo.uri |
– |
URI of the repository to open |
| kite.dataset.name |
– |
Name of the Dataset where records will be written |
| kite.batchSize |
100 |
Number of records to process in each batch |
| kite.rollInterval |
30 |
Maximum wait time (seconds) before data files are released |
| auth.kerberosPrincipal |
– |
Kerberos user principal for secure authentication to HDFS |
| auth.kerberosKeytab |
– |
Kerberos keytab location (local FS) for the principal |
| auth.proxyUser |
– |
The effective user for HDFS actions, if different from
the kerberos principal |
Kafka Sink
This is a Flume Sink implementation that can publish data to a
Kafka topic. One of the objective is to integrate Flume
with Kafka so that pull based processing systems can process the data coming
through various Flume sources. This currently supports Kafka 0.9.x series of releases.
This version of Flume no longer supports Older Versions (0.8.x) of Kafka.
Required properties are marked in bold font.
| Property Name |
Default |
Description |
|---|
| type |
– |
Must be set to org.apache.flume.sink.kafka.KafkaSink |
| kafka.bootstrap.servers |
– |
List of brokers Kafka-Sink will connect to, to get the list of topic partitions
This can be a partial list of brokers, but we recommend at least two for HA.
The format is comma separated list of hostname:port |
| kafka.topic |
default-flume-topic |
The topic in Kafka to which the messages will be published. If this parameter is configured,
messages will be published to this topic.
If the event header contains a “topic” field, the event will be published to that topic
overriding the topic configured here. |
| flumeBatchSize |
100 |
How many messages to process in one batch. Larger batches improve throughput while adding latency. |
| kafka.producer.acks |
1 |
How many replicas must acknowledge a message before its considered successfully written.
Accepted values are 0 (Never wait for acknowledgement), 1 (wait for leader only), -1 (wait for all replicas)
Set this to -1 to avoid data loss in some cases of leader failure. |
| useFlumeEventFormat |
false |
By default events are put as bytes onto the Kafka topic directly from the event body. Set to
true to store events as the Flume Avro binary format. Used in conjunction with the same property
on the KafkaSource or with the parseAsFlumeEvent property on the Kafka Channel this will preserve
any Flume headers for the producing side. |
| Other Kafka Producer Properties |
– |
These properties are used to configure the Kafka Producer. Any producer property supported
by Kafka can be used. The only requirement is to prepend the property name with the prefix
kafka.producer.
For example: kafka.producer.linger.ms |
Note
Kafka Sink uses the topic and key properties from the FlumeEvent headers to send events to Kafka.
If topic exists in the headers, the event will be sent to that specific topic, overriding the topic configured for the Sink.
If key exists in the headers, the key will used by Kafka to partition the data between the topic partitions. Events with same key
will be sent to the same partition. If the key is null, events will be sent to random partitions.
The Kafka sink also provides defaults for the key.serializer(org.apache.kafka.common.serialization.StringSerializer)
and value.serializer(org.apache.kafka.common.serialization.ByteArraySerializer). Modification of these parameters is not recommended.
Deprecated Properties
| Property Name |
Default |
Description |
|---|
| brokerList |
– |
Use kafka.bootstrap.servers |
| topic |
default-flume-topic |
Use kafka.topic |
| batchSize |
100 |
Use kafka.flumeBatchSize |
| requiredAcks |
1 |
Use kafka.producer.acks |
An example configuration of a Kafka sink is given below. Properties starting
with the prefix kafka.producer the Kafka producer. The properties that are passed when creating the Kafka
producer are not limited to the properties given in this example.
Also it is possible to include your custom properties here and access them inside
the preprocessor through the Flume Context object passed in as a method
argument.
a1.sinks.k1.channel = c1
a1.sinks.k1.type = org.apache.flume.sink.kafka.KafkaSink
a1.sinks.k1.kafka.topic = mytopic
a1.sinks.k1.kafka.bootstrap.servers = localhost:9092
a1.sinks.k1.kafka.flumeBatchSize = 20
a1.sinks.k1.kafka.producer.acks = 1
a1.sinks.k1.kafka.producer.linger.ms = 1
a1.sinks.ki.kafka.producer.compression.type = snappy
Custom Sink
A custom sink is your own implementation of the Sink interface. A custom
sink’s class and its dependencies must be included in the agent’s classpath
when starting the Flume agent. The type of the custom sink is its FQCN.
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| channel |
– |
|
| type |
– |
The component type name, needs to be your FQCN |
Example for agent named a1:
a1.channels = c1
a1.sinks = k1
a1.sinks.k1.type = org.example.MySink
a1.sinks.k1.channel = c1
Flume Channels
Channels are the repositories where the events are staged on a agent.
Source adds the events and Sink removes it.
Memory Channel
The events are stored in an in-memory queue with configurable max size. It’s
ideal for flows that need higher throughput and are prepared to lose the staged
data in the event of a agent failures.
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| type |
– |
The component type name, needs to be memory |
| capacity |
100 |
The maximum number of events stored in the channel |
| transactionCapacity |
100 |
The maximum number of events the channel will take from a source or give to a
sink per transaction |
| keep-alive |
3 |
Timeout in seconds for adding or removing an event |
| byteCapacityBufferPercentage |
20 |
Defines the percent of buffer between byteCapacity and the estimated total size
of all events in the channel, to account for data in headers. See below. |
| byteCapacity |
see description |
Maximum total bytes of memory allowed as a sum of all events in this channel.
The implementation only counts the Event body, which is the reason for
providing the byteCapacityBufferPercentage configuration parameter as well.
Defaults to a computed value equal to 80% of the maximum memory available to
the JVM (i.e. 80% of the -Xmx value passed on the command line).
Note that if you have multiple memory channels on a single JVM, and they happen
to hold the same physical events (i.e. if you are using a replicating channel
selector from a single source) then those event sizes may be double-counted for
channel byteCapacity purposes.
Setting this value to 0 will cause this value to fall back to a hard
internal limit of about 200 GB. |
Example for agent named a1:
a1.channels = c1
a1.channels.c1.type = memory
a1.channels.c1.capacity = 10000
a1.channels.c1.transactionCapacity = 10000
a1.channels.c1.byteCapacityBufferPercentage = 20
a1.channels.c1.byteCapacity = 800000
JDBC Channel
The events are stored in a persistent storage that’s backed by a database.
The JDBC channel currently supports embedded Derby. This is a durable channel
that’s ideal for flows where recoverability is important.
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| type |
– |
The component type name, needs to be jdbc |
| db.type |
DERBY |
Database vendor, needs to be DERBY. |
| driver.class |
org.apache.derby.jdbc.EmbeddedDriver |
Class for vendor’s JDBC driver |
| driver.url |
(constructed from other properties) |
JDBC connection URL |
| db.username |
“sa” |
User id for db connection |
| db.password |
– |
password for db connection |
| connection.properties.file |
– |
JDBC Connection property file path |
| create.schema |
true |
If true, then creates db schema if not there |
| create.index |
true |
Create indexes to speed up lookups |
| create.foreignkey |
true |
|
| transaction.isolation |
“READ_COMMITTED” |
Isolation level for db session READ_UNCOMMITTED,
READ_COMMITTED, SERIALIZABLE, REPEATABLE_READ |
| maximum.connections |
10 |
Max connections allowed to db |
| maximum.capacity |
0 (unlimited) |
Max number of events in the channel |
| sysprop.* |
|
DB Vendor specific properties |
| sysprop.user.home |
|
Home path to store embedded Derby database |
Example for agent named a1:
a1.channels = c1
a1.channels.c1.type = jdbc
Kafka Channel
The events are stored in a Kafka cluster (must be installed separately). Kafka provides high availability and
replication, so in case an agent or a kafka broker crashes, the events are immediately available to other sinks
The Kafka channel can be used for multiple scenarios:
* With Flume source and sink - it provides a reliable and highly available channel for events
* With Flume source and interceptor but no sink - it allows writing Flume events into a Kafka topic, for use by other apps
* With Flume sink, but no source - it is a low-latency, fault tolerant way to send events from Kafka to Flume sources such as HDFS, HBase or Solr
This version of Flume requires Kafka version 0.9 or greater due to the reliance on the Kafka clients shipped with that version. The configuration of
the channel has changed compared to previous flume versions.
The configuration parameters are organized as such:
1) Configuration values related to the channel generically are applied at the channel config level, eg: a1.channel.k1.type =
2) Configuration values related to Kafka or how the Channel operates are prefixed with “kafka.”, (this are analgous to CommonClient Configs)eg: a1.channels.k1.kafka.topica1.channels.k1.kafka.bootstrap.serversThis is not dissimilar to how the hdfs sink operates
3) Properties specific to the producer/consumer are prefixed by kafka.producer or kafka.consumer
4) Where possible, the Kafka paramter names are used, eg: bootstrap.servers and acks
This version of flume is backwards-compatible with previous versions, however deprecated properties are indicated in the table below and a warning message
is logged on startup when they are present in the configuration file.
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| type |
– |
The component type name, needs to be org.apache.flume.channel.kafka.KafkaChannel |
| kafka.bootstrap.servers |
– |
List of brokers in the Kafka cluster used by the channel
This can be a partial list of brokers, but we recommend at least two for HA.
The format is comma separated list of hostname:port |
| kafka.topic |
flume-channel |
Kafka topic which the channel will use |
| kafka.consumer.group.id |
flume |
Consumer group ID the channel uses to register with Kafka.
Multiple channels must use the same topic and group to ensure that when one agent fails another can get the data
Note that having non-channel consumers with the same ID can lead to data loss. |
| parseAsFlumeEvent |
true |
Expecting Avro datums with FlumeEvent schema in the channel.
This should be true if Flume source is writing to the channel and false if other producers are
writing into the topic that the channel is using. Flume source messages to Kafka can be parsed outside of Flume by using
org.apache.flume.source.avro.AvroFlumeEvent provided by the flume-ng-sdk artifact |
| migrateZookeeperOffsets |
true |
When no Kafka stored offset is found, look up the offsets in Zookeeper and commit them to Kafka.
This should be true to support seamless Kafka client migration from older versions of Flume. Once migrated this can be set
to false, though that should generally not be required. If no Zookeeper offset is found the kafka.consumer.auto.offset.reset
configuration defines how offsets are handled. |
| pollTimeout |
500 |
The amount of time(in milliseconds) to wait in the “poll()” call of the conumer.
https://kafka.apache.org/090/javadoc/org/apache/kafka/clients/consumer/KafkaConsumer.html#poll(long) |
| kafka.consumer.auto.offset.reset |
latest |
What to do when there is no initial offset in Kafka or if the current offset does not exist any more on the server
(e.g. because that data has been deleted):
earliest: automatically reset the offset to the earliest offset
latest: automatically reset the offset to the latest offset
none: throw exception to the consumer if no previous offset is found for the consumer’s group
anything else: throw exception to the consumer. |
| kafka.producer.security.protocol |
PLAINTEXT |
Set to SASL_PLAINTEXT, SASL_SSL or SSL if writing to Kafka using Kerberos. See below for additional info on Kerberos setup. |
| kafka.consumer.security.protocol |
PLAINTEXT |
Same as kafka.producer.security.protocol but for reading/consuming from Kafka. |
| more producer/consumer security props |
|
If using SASL_SSL or SSL, refer to Kafka security for additional
properties that need to be set on producer/consumer. |
Deprecated Properties
| Property Name |
Default |
Description |
|---|
| brokerList |
– |
List of brokers in the Kafka cluster used by the channel
This can be a partial list of brokers, but we recommend at least two for HA.
The format is comma separated list of hostname:port |
| topic |
flume-channel |
Use kafka.topic |
| groupId |
flume |
Use kafka.consumer.group.id |
| readSmallestOffset |
false |
Use kafka.consumer.auto.offset.reset |
Note
Due to the way the channel is load balanced, there may be duplicate events when the agent first starts up
Example for agent named a1:
a1.channels.channel1.type = org.apache.flume.channel.kafka.KafkaChannel
a1.channels.channel1.kafka.bootstrap.servers = kafka-1:9092,kafka-2:9092,kafka-3:9092
a1.channels.channel1.kafka.topic = channel1
a1.channels.channel1.kafka.consumer.group.id = flume-consumer
Kerberos and Kafka Channel:
To use Kafka channel with a Kafka cluster secured with Kerberos, set the producer/consumer.security.protocol properties noted above for producer and/or consumer.
The Kerberos keytab and principal to be used is specified in a JAAS file’s “KafkaClient” section. See Kafka doc
for info on the JAAS file contents. The location of this JAAS file is specified via JAVA_OPTS using -Djava.security.auth.login.config=/path/to/kafka_jaas.conf (in flume-env.sh)
Sample secure configuration using SASL_PLAINTEXT.
a1.channels.channel1.type = org.apache.flume.channel.kafka.KafkaChannel
a1.channels.channel1.kafka.bootstrap.servers = kafka-1:9092,kafka-2:9092,kafka-3:9092
a1.channels.channel1.kafka.topic = channel1
a1.channels.channel1.kafka.consumer.group.id = flume-consumer
a1.channels.channel1.kafka.producer.security.protocol = SASL_PLAINTEXT
a1.channels.channel1.kafka.consumer.security.protocol = SASL_PLAINTEXT
Sample JAAS file
KafkaClient {
com.sun.security.auth.module.Krb5LoginModule required
useKeyTab=true
storeKey=true
serviceName="kafka"
keyTab="/path/to/keytabs/testuser1.keytab"
principal="testuser1/kafka1.example.com";
};
Sample flume-env.sh
export JAVA_HOME=/path/java-home/
export JAVA_OPTS="-Djava.security.auth.login.config=/path/to/kafka_jaas.conf"
File Channel
Required properties are in bold.
| Property Name Default |
Description |
|
|---|
| type |
– |
The component type name, needs to be file. |
| checkpointDir |
~/.flume/file-channel/checkpoint |
The directory where checkpoint file will be stored |
| useDualCheckpoints |
false |
Backup the checkpoint. If this is set to true, backupCheckpointDir must be set |
| backupCheckpointDir |
– |
The directory where the checkpoint is backed up to. This directory must not be the same as the data directories or the checkpoint directory |
| dataDirs |
~/.flume/file-channel/data |
Comma separated list of directories for storing log files. Using multiple directories on separate disks can improve file channel peformance |
| transactionCapacity |
10000 |
The maximum size of transaction supported by the channel |
| checkpointInterval |
30000 |
Amount of time (in millis) between checkpoints |
| maxFileSize |
2146435071 |
Max size (in bytes) of a single log file |
| minimumRequiredSpace |
524288000 |
Minimum Required free space (in bytes). To avoid data corruption, File Channel stops accepting take/put requests when free space drops below this value |
| capacity |
1000000 |
Maximum capacity of the channel |
| keep-alive |
3 |
Amount of time (in sec) to wait for a put operation |
| use-log-replay-v1 |
false |
Expert: Use old replay logic |
| use-fast-replay |
false |
Expert: Replay without using queue |
| checkpointOnClose |
true |
Controls if a checkpoint is created when the channel is closed. Creating a checkpoint on close speeds up subsequent startup of the file channel by avoiding replay. |
| encryption.activeKey |
– |
Key name used to encrypt new data |
| encryption.cipherProvider |
– |
Cipher provider type, supported types: AESCTRNOPADDING |
| encryption.keyProvider |
– |
Key provider type, supported types: JCEKSFILE |
| encryption.keyProvider.keyStoreFile |
– |
Path to the keystore file |
| encrpytion.keyProvider.keyStorePasswordFile |
– |
Path to the keystore password file |
| encrpytion.keyProvider.keyStorePasswordFileType |
TEXT |
Type of keystore password file. “TEXT” indicates simple raw text. “AES” indicates file is created using ‘flume-ng password’ command. |
| encryption.keyProvider.keys |
– |
List of all keys (e.g. history of the activeKey setting) |
| encyption.keyProvider.keys.*.passwordFile |
– |
Path to the optional key password file |
Note
By default the File Channel uses paths for checkpoint and data
directories that are within the user home as specified above.
As a result if you have more than one File Channel instances
active within the agent, only one will be able to lock the
directories and cause the other channel initialization to fail.
It is therefore necessary that you provide explicit paths to
all the configured channels, preferably on different disks.
Furthermore, as file channel will sync to disk after every commit,
coupling it with a sink/source that batches events together may
be necessary to provide good performance where multiple disks are
not available for checkpoint and data directories.
Example for agent named a1:
a1.channels = c1
a1.channels.c1.type = file
a1.channels.c1.checkpointDir = /mnt/flume/checkpoint
a1.channels.c1.dataDirs = /mnt/flume/data
Encryption
Below is a few sample configurations:
Generating a key with a password seperate from the key store password:
keytool -genseckey -alias key-0 -keypass keyPassword -keyalg AES \
-keysize 128 -validity 9000 -keystore test.keystore \
-storetype jceks -storepass keyStorePassword
Generating a key with the password the same as the key store password:
keytool -genseckey -alias key-1 -keyalg AES -keysize 128 -validity 9000 \
-keystore src/test/resources/test.keystore -storetype jceks \
-storepass keyStorePassword
a1.channels.c1.encryption.activeKey = key-0
a1.channels.c1.encryption.cipherProvider = AESCTRNOPADDING
a1.channels.c1.encryption.keyProvider = key-provider-0
a1.channels.c1.encryption.keyProvider = JCEKSFILE
a1.channels.c1.encryption.keyProvider.keyStoreFile = /path/to/my.keystore
a1.channels.c1.encryption.keyProvider.keyStorePasswordFile = /path/to/my.keystore.password
a1.channels.c1.encryption.keyProvider.keys = key-0
Let’s say you have aged key-0 out and new files should be encrypted with key-1:
a1.channels.c1.encryption.activeKey = key-1
a1.channels.c1.encryption.cipherProvider = AESCTRNOPADDING
a1.channels.c1.encryption.keyProvider = JCEKSFILE
a1.channels.c1.encryption.keyProvider.keyStoreFile = /path/to/my.keystore
a1.channels.c1.encryption.keyProvider.keyStorePasswordFile = /path/to/my.keystore.password
a1.channels.c1.encryption.keyProvider.keys = key-0 key-1
The same scenerio as above, however key-0 has its own password:
a1.channels.c1.encryption.activeKey = key-1
a1.channels.c1.encryption.cipherProvider = AESCTRNOPADDING
a1.channels.c1.encryption.keyProvider = JCEKSFILE
a1.channels.c1.encryption.keyProvider.keyStoreFile = /path/to/my.keystore
a1.channels.c1.encryption.keyProvider.keyStorePasswordFile = /path/to/my.keystore.password
a1.channels.c1.encryption.keyProvider.keys = key-0 key-1
a1.channels.c1.encryption.keyProvider.keys.key-0.passwordFile = /path/to/key-0.password
Spillable Memory Channel
The events are stored in an in-memory queue and on disk. The in-memory queue serves as the primary store and the disk as overflow.
The disk store is managed using an embedded File channel. When the in-memory queue is full, additional incoming events are stored in
the file channel. This channel is ideal for flows that need high throughput of memory channel during normal operation, but at the
same time need the larger capacity of the file channel for better tolerance of intermittent sink side outages or drop in drain rates.
The throughput will reduce approximately to file channel speeds during such abnormal situations. In case of an agent crash or restart,
only the events stored on disk are recovered when the agent comes online. This channel is currently experimental and
not recommended for use in production.
Required properties are in bold. Please refer to file channel for additional required properties.
| Property Name |
Default |
Description |
|---|
| type |
– |
The component type name, needs to be SPILLABLEMEMORY |
| memoryCapacity |
10000 |
Maximum number of events stored in memory queue. To disable use of in-memory queue, set this to zero. |
| overflowCapacity |
100000000 |
Maximum number of events stored in overflow disk (i.e File channel). To disable use of overflow, set this to zero. |
| overflowTimeout |
3 |
The number of seconds to wait before enabling disk overflow when memory fills up. |
| byteCapacityBufferPercentage |
20 |
Defines the percent of buffer between byteCapacity and the estimated total size
of all events in the channel, to account for data in headers. See below. |
| byteCapacity |
see description |
Maximum bytes of memory allowed as a sum of all events in the memory queue.
The implementation only counts the Event body, which is the reason for
providing the byteCapacityBufferPercentage configuration parameter as well.
Defaults to a computed value equal to 80% of the maximum memory available to
the JVM (i.e. 80% of the -Xmx value passed on the command line).
Note that if you have multiple memory channels on a single JVM, and they happen
to hold the same physical events (i.e. if you are using a replicating channel
selector from a single source) then those event sizes may be double-counted for
channel byteCapacity purposes.
Setting this value to 0 will cause this value to fall back to a hard
internal limit of about 200 GB. |
| avgEventSize |
500 |
Estimated average size of events, in bytes, going into the channel |
| <file channel properties> |
see file channel |
Any file channel property with the exception of ‘keep-alive’ and ‘capacity’ can be used.
The keep-alive of file channel is managed by Spillable Memory Channel. Use ‘overflowCapacity’
to set the File channel’s capacity. |
In-memory queue is considered full if either memoryCapacity or byteCapacity limit is reached.
Example for agent named a1:
a1.channels = c1
a1.channels.c1.type = SPILLABLEMEMORY
a1.channels.c1.memoryCapacity = 10000
a1.channels.c1.overflowCapacity = 1000000
a1.channels.c1.byteCapacity = 800000
a1.channels.c1.checkpointDir = /mnt/flume/checkpoint
a1.channels.c1.dataDirs = /mnt/flume/data
To disable the use of the in-memory queue and function like a file channel:
a1.channels = c1
a1.channels.c1.type = SPILLABLEMEMORY
a1.channels.c1.memoryCapacity = 0
a1.channels.c1.overflowCapacity = 1000000
a1.channels.c1.checkpointDir = /mnt/flume/checkpoint
a1.channels.c1.dataDirs = /mnt/flume/data
To disable the use of overflow disk and function purely as a in-memory channel:
a1.channels = c1
a1.channels.c1.type = SPILLABLEMEMORY
a1.channels.c1.memoryCapacity = 100000
a1.channels.c1.overflowCapacity = 0
Pseudo Transaction Channel
Warning
The Pseudo Transaction Channel is only for unit testing purposes
and is NOT meant for production use.
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| type |
– |
The component type name, needs to be org.apache.flume.channel.PseudoTxnMemoryChannel |
| capacity |
50 |
The max number of events stored in the channel |
| keep-alive |
3 |
Timeout in seconds for adding or removing an event |
Custom Channel
A custom channel is your own implementation of the Channel interface. A
custom channel’s class and its dependencies must be included in the agent’s
classpath when starting the Flume agent. The type of the custom channel is
its FQCN.
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| type |
– |
The component type name, needs to be a FQCN |
Example for agent named a1:
a1.channels = c1
a1.channels.c1.type = org.example.MyChannel
Flume Sink Processors
Sink groups allow users to group multiple sinks into one entity.
Sink processors can be used to provide load balancing capabilities over all
sinks inside the group or to achieve fail over from one sink to another in
case of temporal failure.
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| sinks |
– |
Space-separated list of sinks that are participating in the group |
| processor.type |
default |
The component type name, needs to be default, failover or load_balance |
Example for agent named a1:
a1.sinkgroups = g1
a1.sinkgroups.g1.sinks = k1 k2
a1.sinkgroups.g1.processor.type = load_balance
Default Sink Processor
Default sink processor accepts only a single sink. User is not forced
to create processor (sink group) for single sinks. Instead user can follow
the source - channel - sink pattern that was explained above in this user
guide.
Failover Sink Processor
Failover Sink Processor maintains a prioritized list of sinks, guaranteeing
that so long as one is available events will be processed (delivered).
The failover mechanism works by relegating failed sinks to a pool where
they are assigned a cool down period, increasing with sequential failures
before they are retried. Once a sink successfully sends an event, it is
restored to the live pool.
To configure, set a sink groups processor to failover and set
priorities for all individual sinks. All specified priorities must
be unique. Furthermore, upper limit to failover time can be set
(in milliseconds) using maxpenalty property.
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| sinks |
– |
Space-separated list of sinks that are participating in the group |
| processor.type |
default |
The component type name, needs to be failover |
| processor.priority.<sinkName> |
– |
<sinkName> must be one of the sink instances associated with the current sink group |
| processor.maxpenalty |
30000 |
(in millis) |
Example for agent named a1:
a1.sinkgroups = g1
a1.sinkgroups.g1.sinks = k1 k2
a1.sinkgroups.g1.processor.type = failover
a1.sinkgroups.g1.processor.priority.k1 = 5
a1.sinkgroups.g1.processor.priority.k2 = 10
a1.sinkgroups.g1.processor.maxpenalty = 10000
Load balancing Sink Processor
Load balancing sink processor provides the ability to load-balance flow over
multiple sinks. It maintains an indexed list of active sinks on which the
load must be distributed. Implementation supports distributing load using
either via round_robin or random selection mechanisms.
The choice of selection mechanism defaults to round_robin type,
but can be overridden via configuration. Custom selection mechanisms are
supported via custom classes that inherits from AbstractSinkSelector.
When invoked, this selector picks the next sink using its configured selection
mechanism and invokes it. For round_robin and random In case the selected sink
fails to deliver the event, the processor picks the next available sink via
its configured selection mechanism. This implementation does not blacklist
the failing sink and instead continues to optimistically attempt every
available sink. If all sinks invocations result in failure, the selector
propagates the failure to the sink runner.
If backoff is enabled, the sink processor will blacklist
sinks that fail, removing them for selection for a given timeout. When the
timeout ends, if the sink is still unresponsive timeout is increased
exponentially to avoid potentially getting stuck in long waits on unresponsive
sinks. With this disabled, in round-robin all the failed sinks load will be
passed to the next sink in line and thus not evenly balanced
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| processor.sinks |
– |
Space-separated list of sinks that are participating in the group |
| processor.type |
default |
The component type name, needs to be load_balance |
| processor.backoff |
false |
Should failed sinks be backed off exponentially. |
| processor.selector |
round_robin |
Selection mechanism. Must be either round_robin, random
or FQCN of custom class that inherits from AbstractSinkSelector |
| processor.selector.maxTimeOut |
30000 |
Used by backoff selectors to limit exponential backoff (in milliseconds) |
Example for agent named a1:
a1.sinkgroups = g1
a1.sinkgroups.g1.sinks = k1 k2
a1.sinkgroups.g1.processor.type = load_balance
a1.sinkgroups.g1.processor.backoff = true
a1.sinkgroups.g1.processor.selector = random
Custom Sink Processor
Custom sink processors are not supported at the moment.
Flume Interceptors
Flume has the capability to modify/drop events in-flight. This is done with the help of interceptors. Interceptors
are classes that implement org.apache.flume.interceptor.Interceptor interface. An interceptor can
modify or even drop events based on any criteria chosen by the developer of the interceptor. Flume supports
chaining of interceptors. This is made possible through by specifying the list of interceptor builder class names
in the configuration. Interceptors are specified as a whitespace separated list in the source configuration.
The order in which the interceptors are specified is the order in which they are invoked.
The list of events returned by one interceptor is passed to the next interceptor in the chain. Interceptors
can modify or drop events. If an interceptor needs to drop events, it just does not return that event in
the list that it returns. If it is to drop all events, then it simply returns an empty list. Interceptors
are named components, here is an example of how they are created through configuration:
a1.sources = r1
a1.sinks = k1
a1.channels = c1
a1.sources.r1.interceptors = i1 i2
a1.sources.r1.interceptors.i1.type = org.apache.flume.interceptor.HostInterceptor$Builder
a1.sources.r1.interceptors.i1.preserveExisting = false
a1.sources.r1.interceptors.i1.hostHeader = hostname
a1.sources.r1.interceptors.i2.type = org.apache.flume.interceptor.TimestampInterceptor$Builder
a1.sinks.k1.filePrefix = FlumeData.%{CollectorHost}.%Y-%m-%d
a1.sinks.k1.channel = c1
Note that the interceptor builders are passed to the type config parameter. The interceptors are themselves
configurable and can be passed configuration values just like they are passed to any other configurable component.
In the above example, events are passed to the HostInterceptor first and the events returned by the HostInterceptor
are then passed along to the TimestampInterceptor. You can specify either the fully qualified class name (FQCN)
or the alias timestamp. If you have multiple collectors writing to the same HDFS path, then you could also use
the HostInterceptor.
Timestamp Interceptor
This interceptor inserts into the event headers, the time in millis at which it processes the event. This interceptor
inserts a header with key timestamp whose value is the relevant timestamp. This interceptor
can preserve an existing timestamp if it is already present in the configuration.
| Property Name |
Default |
Description |
|---|
| type |
– |
The component type name, has to be timestamp or the FQCN |
| preserveExisting |
false |
If the timestamp already exists, should it be preserved - true or false |
Example for agent named a1:
a1.sources = r1
a1.channels = c1
a1.sources.r1.channels = c1
a1.sources.r1.type = seq
a1.sources.r1.interceptors = i1
a1.sources.r1.interceptors.i1.type = timestamp
Host Interceptor
This interceptor inserts the hostname or IP address of the host that this agent is running on. It inserts a header
with key host or a configured key whose value is the hostname or IP address of the host, based on configuration.
| Property Name |
Default |
Description |
|---|
| type |
– |
The component type name, has to be host |
| preserveExisting |
false |
If the host header already exists, should it be preserved - true or false |
| useIP |
true |
Use the IP Address if true, else use hostname. |
| hostHeader |
host |
The header key to be used. |
Example for agent named a1:
a1.sources = r1
a1.channels = c1
a1.sources.r1.interceptors = i1
a1.sources.r1.interceptors.i1.type = host
a1.sources.r1.interceptors.i1.hostHeader = hostname
Static Interceptor
Static interceptor allows user to append a static header with static value to all events.
The current implementation does not allow specifying multiple headers at one time. Instead user might chain
multiple static interceptors each defining one static header.
| Property Name |
Default |
Description |
|---|
| type |
– |
The component type name, has to be static |
| preserveExisting |
true |
If configured header already exists, should it be preserved - true or false |
| key |
key |
Name of header that should be created |
| value |
value |
Static value that should be created |
Example for agent named a1:
a1.sources = r1
a1.channels = c1
a1.sources.r1.channels = c1
a1.sources.r1.type = seq
a1.sources.r1.interceptors = i1
a1.sources.r1.interceptors.i1.type = static
a1.sources.r1.interceptors.i1.key = datacenter
a1.sources.r1.interceptors.i1.value = NEW_YORK
UUID Interceptor
This interceptor sets a universally unique identifier on all events that are intercepted. An example UUID is b5755073-77a9-43c1-8fad-b7a586fc1b97, which represents a 128-bit value.
Consider using UUIDInterceptor to automatically assign a UUID to an event if no application level unique key for the event is available. It can be important to assign UUIDs to events as soon as they enter the Flume network; that is, in the first Flume Source of the flow. This enables subsequent deduplication of events in the face of replication and redelivery in a Flume network that is designed for high availability and high performance. If an application level key is available, this is preferable over an auto-generated UUID because it enables subsequent updates and deletes of event in data stores using said well known application level key.
| Property Name |
Default |
Description |
|---|
| type |
– |
The component type name has to be org.apache.flume.sink.solr.morphline.UUIDInterceptor$Builder |
| headerName |
id |
The name of the Flume header to modify |
| preserveExisting |
true |
If the UUID header already exists, should it be preserved - true or false |
| prefix |
“” |
The prefix string constant to prepend to each generated UUID |
Morphline Interceptor
This interceptor filters the events through a morphline configuration file that defines a chain of transformation commands that pipe records from one command to another.
For example the morphline can ignore certain events or alter or insert certain event headers via regular expression based pattern matching, or it can auto-detect and set a MIME type via Apache Tika on events that are intercepted. For example, this kind of packet sniffing can be used for content based dynamic routing in a Flume topology.
MorphlineInterceptor can also help to implement dynamic routing to multiple Apache Solr collections (e.g. for multi-tenancy).
Currently, there is a restriction in that the morphline of an interceptor must not generate more than one output record for each input event. This interceptor is not intended for heavy duty ETL processing - if you need this consider moving ETL processing from the Flume Source to a Flume Sink, e.g. to a MorphlineSolrSink.
Required properties are in bold.
| Property Name |
Default |
Description |
|---|
| type |
– |
The component type name has to be org.apache.flume.sink.solr.morphline.MorphlineInterceptor$Builder |
| morphlineFile |
– |
The relative or absolute path on the local file system to the morphline configuration file. Example: /etc/flume-ng/conf/morphline.conf |
| morphlineId |
null |
Optional name used to identify a morphline if there are multiple morphlines in a morphline config file |
Sample flume.conf file:
a1.sources.avroSrc.interceptors = morphlineinterceptor
a1.sources.avroSrc.interceptors.morphlineinterceptor.type = org.apache.flume.sink.solr.morphline.MorphlineInterceptor$Builder
a1.sources.avroSrc.interceptors.morphlineinterceptor.morphlineFile = /etc/flume-ng/conf/morphline.conf
a1.sources.avroSrc.interceptors.morphlineinterceptor.morphlineId = morphline1
Regex Filtering Interceptor
This interceptor filters events selectively by interpreting the event body as text and matching the text against a configured regular expression.
The supplied regular expression can be used to include events or exclude events.
| Property Name |
Default |
Description |
|---|
| type |
– |
The component type name has to be regex_filter |
| regex |
”.*” |
Regular expression for matching against events |
| excludeEvents |
false |
If true, regex determines events to exclude, otherwise regex determines
events to include. |
Example 1:
If the Flume event body contained 1:2:3.4foobar5 and the following configuration was used
a1.sources.r1.interceptors.i1.regex = (\\d):(\\d):(\\d)
a1.sources.r1.interceptors.i1.serializers = s1 s2 s3
a1.sources.r1.interceptors.i1.serializers.s1.name = one
a1.sources.r1.interceptors.i1.serializers.s2.name = two
a1.sources.r1.interceptors.i1.serializers.s3.name = three
The extracted event will contain the same body but the following headers will have been added one=>1, two=>2, three=>3
Example 2:
If the Flume event body contained 2012-10-18 18:47:57,614 some log line and the following configuration was used
a1.sources.r1.interceptors.i1.regex = ^(?:\\n)?(\\d\\d\\d\\d-\\d\\d-\\d\\d\\s\\d\\d:\\d\\d)
a1.sources.r1.interceptors.i1.serializers = s1
a1.sources.r1.interceptors.i1.serializers.s1.type = org.apache.flume.interceptor.RegexExtractorInterceptorMillisSerializer
a1.sources.r1.interceptors.i1.serializers.s1.name = timestamp
a1.sources.r1.interceptors.i1.serializers.s1.pattern = yyyy-MM-dd HH:mm
the extracted event will contain the same body but the following headers will have been added timestamp=>1350611220000