Editing users
After you create a user, you can assign policies and roles to the users.
-
Click Administration from the left navigation in the
Cloudera Edge Management UI.
The Administration page appears.
-
In the Users/Groups tab, click the edit icon beside a
user to edit the user.
The user page appears as shown in the following image:
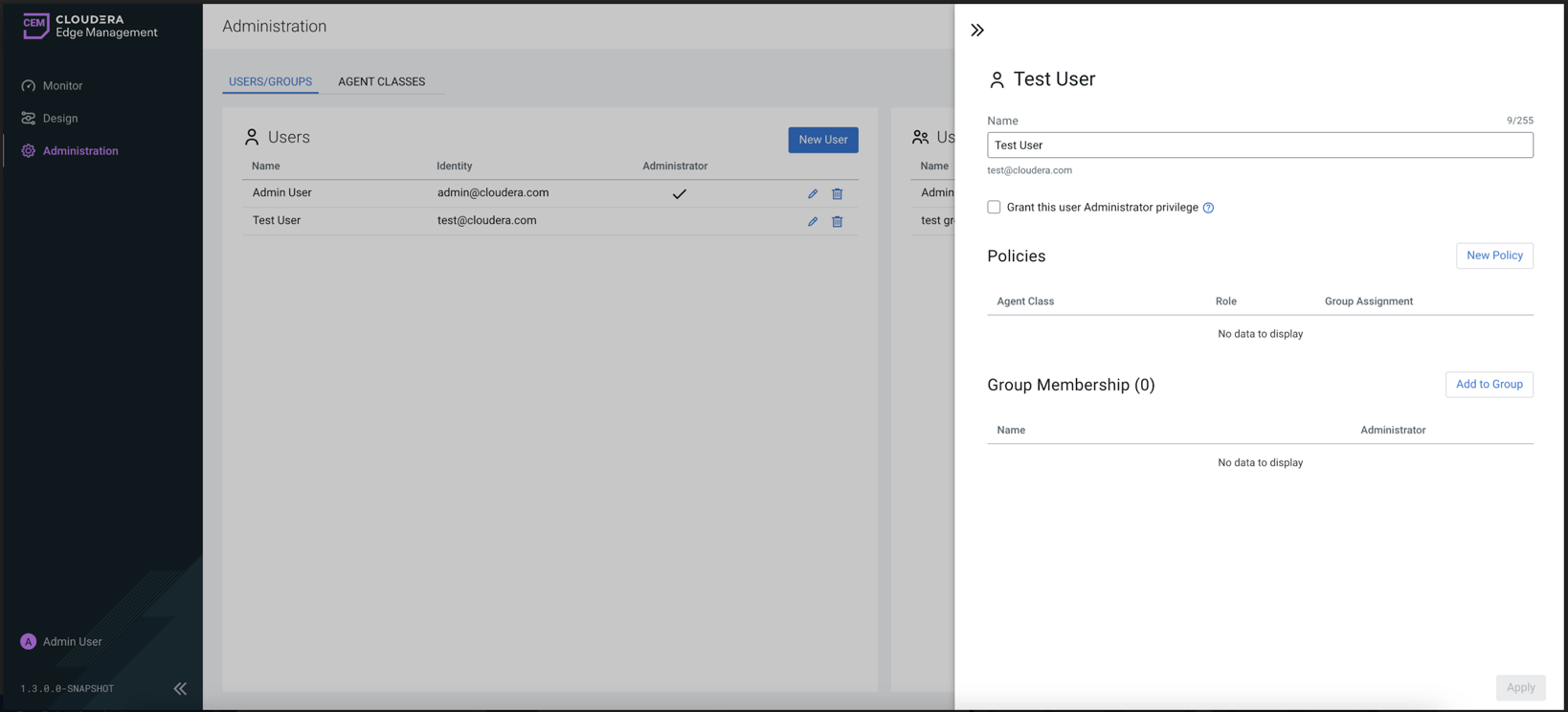
- Edit the name of the user.
- Click the Grant this user Administrator privilege checkbox to grant administrator privileges to the given user.
- Click New Policy to assign policies to the given user (specific role to the given agent class).
- Click Add to Group to add a given user to a group (all of the roles from the group are inherited by the user).
- Click Apply.


